HAOI2007 反素数ant

Time Limit: 10 Sec Memory Limit: 162 MB

Description

　　对于任何正整数x，其约数的个数记作g(x)。例如g(1)=1、g(6)=4。如果某个正整数x满足：g(x)>g(i) 0<i<x，则称x为反质数。例如，整数1，2，4，6等都是反质数。现在给定一个数N，你能求出不超过N的最大的反质数么？

Input

一个数N（1<=N<=2,000,000,000）。

Output

不超过N的最大的反质数。

Sample Input

1000

Sample Output

840

简要题解

首先反质数一定要保证(g(x)>g(i) 0<i<x)，那么我们看这个图像

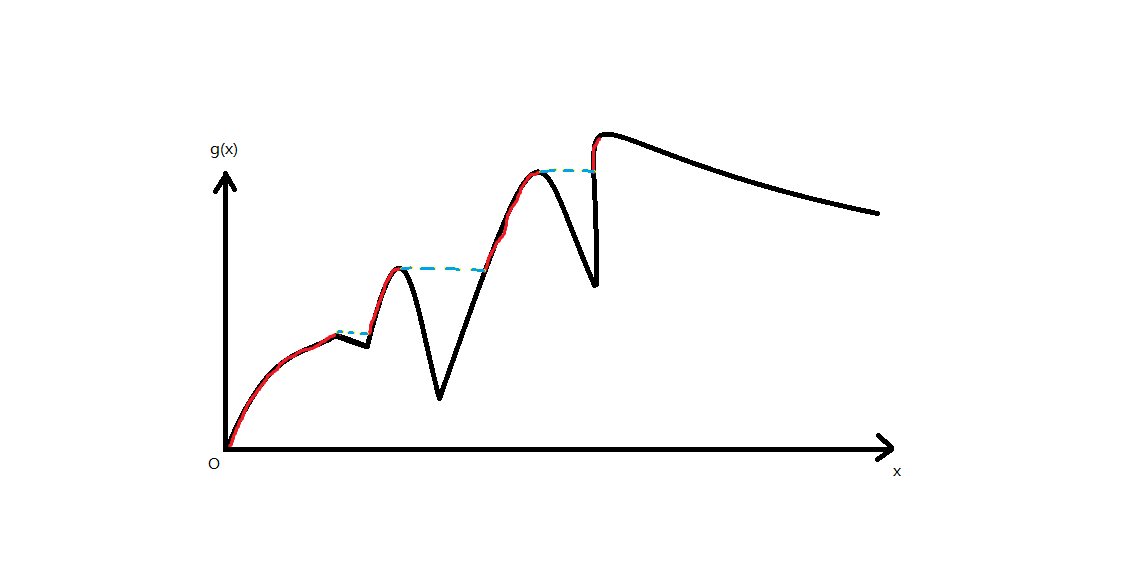
我们假设这个是g(x)的图像，红色部分的图像是反素数的位置，那么我们通过观察可一发现，随着x增大，若x是反素数，那么g(x)也是递增的。我们可以发现，最大的反素数一定是拥有约数最多的数中最小的。
对于一个数(x)，我们把它表示为(p_1^{k_1} cdot p_2^{k_2} cdot p_3^{k_3} cdot ... (p_i ext{为质数，且}p_1<p_2<...))，那么我们可以发现，(2^{30}=1073741824<10^9)，(2^{31}=2147483648>10^9)，所以哪怕x就只是最小的质数——2——的31次方，都会超出n的最大范围，所以就算x只是2的整次方，质数都最多只能是30。因此，(sumlimits_{i=1}^ik_i < 30)。
另外，我们可以证明这些底数(p_i)一定是连续的质数，这些指数(k_i)一定是随i的增大而不递增的。我们假设(i<j k_i<k_j)，则我们可以交换它们的质数，可以得到一个(x'<x)，但是却和x拥有一样多的约数，显然x不可能是反素数。因此，一个反素数质因数分解后的指数应随底数递增而不递增。同时我们可以有这样的结论引申出另一个结论——一旦有一个(k_i)值为0，也就是x不含有(p_i)这个质因数，那么(k_j j>i)也都应该都为0，即x也应该不存在(p_j)这个质因数，也就是说，这些底数(p_i)一定是连续的质数。
那么我们考虑，把最小的10个质数相乘后的积为(6469693230>10^9)，所以反素数x最多只能拥有10个最小的质因子。
经过上述的讨论，我们可以把结论总结一下了。

1. 最大的反素数即是拥有约数最多的数中最小的。
2. 1-N中任何一个数的指数之和不会超过30
3. 反素数x的质因子一定是连续的最小的质因子。
4. 反素数x最多只能拥有10个最小的质因子。
5. 反素数x的质因子的指数单调不递增

有了这些限制，我们可以直接dfs枚举每一个质因子的指数，判断这样的指数符不符合上述标准，同时用乘法计数原理记录g值。最后我们每得出一个数，都把g值和ans比较，若g(x)>ans则直接替换，如果等于ans并且x的值小于ans对应的x值，也可以换过去。最后输出答案即可。

#include<cstdio>
#include<algorithm>
#include<cmath>
#include<cstring>
using namespace std;
typedef long long ll;
namespace io {
    const int SIZE = (1 << 21) + 1;char ibuf[SIZE], *iS, *iT, obuf[SIZE], *oS = obuf, *oT = oS + SIZE - 1, c, qu[55]; int f, qr;
    #define gc() (iS==iT?(iT=(iS=ibuf)+fread(ibuf,1,SIZE,stdin),(iS==iT?EOF:*iS++)):*iS++)
    inline void flush(){fwrite(obuf,1,oS-obuf,stdout);oS=obuf;}
    inline void putc(char x){*oS++=x;if(oS==oT)flush();}
    template<class I>inline void gi (I &x) {for(f=1,c=gc();c<'0'||c>'9';c=gc())if(c=='-')f=-1;for(x=0;c<='9'&&c>='0';c=gc())x=x*10+(c&15);x*=f;}
    template<class I>inline void print(I x){if(!x)putc('0');if(x<0)putc('-'),x=-x;while(x)qu[++qr]=x%10+'0',x/=10;while(qr)putc(qu[qr--]);}
    struct Flusher_ {~Flusher_(){flush();}}io_flusher_;
}

const int maxn=2e9+7,p[]={1,2,3,5,7,11,13,17,19,23,29};//错误笔记：一开始这里把p[4]给打成4
int n,cnt,ans,tns;

inline int min(int x,int y){return x<y?x:y;}
inline void dfs(int x,int num,int g,int pt){
	ll s=1;
	for(register int i=0;i<=pt;++i)if((ll)num*s<=n){
		cnt+=i;
		if(x<10)dfs(x+1,num*s,g*(i+1),min(i,30-cnt));else if(g*(i+1)>tns||(g*(i+1)==tns&&num*s<ans))ans=num*s,tns=g*(i+1);
		cnt-=i;s*=p[x];
	}
}

int main(){
	#ifndef ONLINE_JUDGE
		freopen("ant.in","r",stdin);freopen("ant.out","w",stdout);
	#endif
	io::gi(n);dfs(1,1,1,30);io::print(ans);io::putc('
');
}