【堆/排序】堆排序的两种建堆方法

buildMaxHeap方法

     buildMaxHeap方法的流程简单概括起来就是一句话，从A.length / 2一直到根结点进行maxHeapify调整。下面是图解。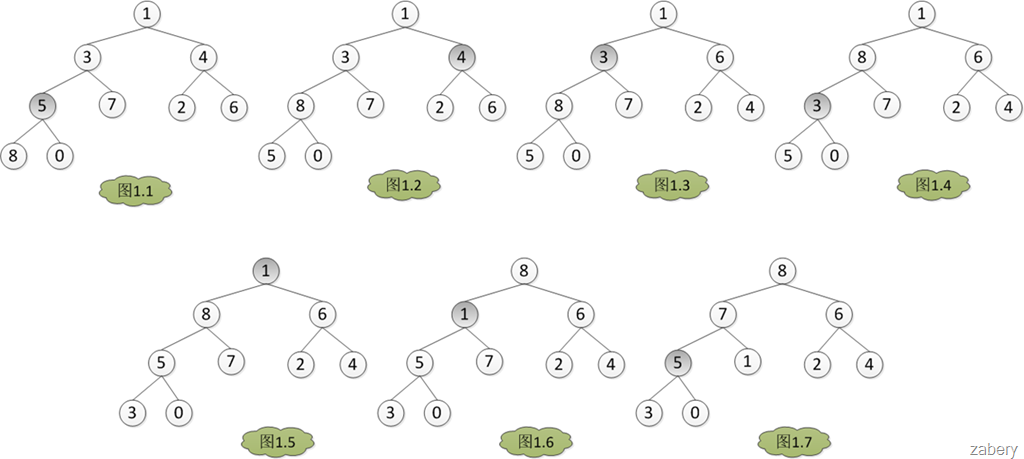

Java代码  

public static void maxHeapify(int[] a, int i, int length)  
{  
    int l = left(i);  
    int r = right(i);  
    int largest = i;  
    while(true)  
    {  
        if(l < length && a[l] > a[i])  
                largest = l;  
        if(r < length && a[r] > a[largest])  
                largest = r;  
        if(i != largest)  
            swap(a, i, largest);  
        else  
            break;  
        i = largest;  
        l = left(largest);  
        r = right(largest);  
    }  
}  
  
public static void buildMaxHeap(int[] a)  
{  
    for(int i = a.length / 2; i >= 0; i--)  
        maxHeapify(a, i, a.length);  
}  

运行时间分析

    粗粗来看前面buildmaxheap的时间复杂度，每次maxHeapify调整需要的时间为lg(n), 总共要遍历的元素有N/2个，所以大致的运行时间复杂度为O(nlgn).

    如果我们更进一步分析，会发现它的实际情况会更理想一点。首先一个，我们从第a.length/2个元素开始执行maxHeapify，最开始这一层的元素只有一个子结点，也就是说，就算要调整，顶多一次就搞定了，不需要走lgn这么多步。

    要做进一步的分析，我们可以先思考一下我们要建的这个完全二叉树堆的几个特性。以如下图为例：

    我们看这棵二叉树，它必须保证每一层填满之后才能去填充下一层。而且，如果从根结点开始计数，往下第i层的元素如果不是最后一层的话，这一层的元素数量为2**i(2的i次方)。这样，对于一棵高为h的二叉树，它的所有结点数目就等于前面完全填满的层元素加上最下面一层的元素。

    为什么要把他们分开来计数呢？是因为最下面一层的元素有一个变动的范围，作为一棵高度为h的树，最下面一层的元素最少可以是1，最大可以是把整层填充满，也就是2**(h+1)。这样，他们求和的结果就是最少为2**h，最大为2**(h+1)。

所以假设堆的元素数量为n的话，我们就可以推出：

 

 结合这一步分析，我们可以得到: h <= lgn < h + 1。

结论1：

我们可以发现一个n个元素的树，它的高度相当于logn（向下取整）。

我们再来看我们分析的第二个结论。对应树每一个高度的一层，该有多少个元素呢？假设高度为1的那一层他们的元素个数为k，那么他们的访问时间复杂度为O(k)。根据前面的分析，我们还发现一个情况，就是如果从根结点开始计数，往下第i层的元素如果不是最后一层的话，这一层的元素数量为2**i(2的i次方)。正好这个第i层就相当于树的总高度减去当前层的结点的高度。假设第i层的高度为h，那么也就是i = lgn - h。

结论2：

这一层的元素数量为：

 那么他们所有元素的运算时间总和为如下：

 根据如下公式：

 

则有：

 

 现在，我们发现，buildMaxHeap方法的时间复杂度实际上为O(n).

maxHeapInsert方法

     maxHeapInsert方法和前面的办法不一样。它可以假定我们事先不知道有多少个元素，通过不断往堆里面插入元素进行调整来构建堆。

它的大致步骤如下：

1. 首先增加堆的长度，在最末尾的地方加入最新插入的元素。

2. 比较当前元素和它的父结点值，如果比父结点值大，则交换两个元素，否则返回。

3. 重复步骤2.

这个过程对应的代码实现如下：

Java代码  

public void heapIncreaseKey(int i, int key) throws Exception  
{  
    if(key < a[i])  
        throw new Exception("new key is small than current key");  
    a[i] = key;  
    while(i > 0 && a[parent(i)] < a[i])  
    {  
        swap(i, parent(i));  
        i = parent(i);  
    }  
}  
  
public void maxHeapInsert(int key) throws Exception  
{  
    heapSize++;  
    a[heapSize - 1] = Integer.MIN_VALUE;  
    heapIncreaseKey(heapSize - 1, key);  
}  

    这里的parent()方法是用来求当前结点的父结点。详细的实现可以参考后面附件里的代码。

    这里，我们也可以分析一下插入建堆的时间复杂度。我们先看最理想的情况，假设每次插入的元素都是严格递减的，那么每个元素只需要和它的父结点比较一次。那么其最优情况就是n。

   对于最坏的情况下，每次新增加一个元素都需要调整到它的根结点。而这个长度为lgn。那么它的时间复杂度为如下公式：

 这样，插入建堆的时间复杂度为nlgn。

 总结

    常用的建堆方法主要用于堆元素已经确定好的情况，而插入建堆的过程主要用于动态的增加元素来建堆。插入建堆的过程也常用于建立优先队列的应用。这些可以根据具体的时间情况来选取。