java数据结构与算法之栈（Stack）设计与实现

本篇是java数据结构与算法的第4篇，从本篇开始我们将来了解栈的设计与实现，以下是本篇的相关知识点：

• 栈的抽象数据类型
• 顺序栈的设计与实现
• 链式栈的设计与实现
• 栈的应用

栈的抽象数据类型

栈是一种用于存储数据的简单数据结构，有点类似链表或者顺序表（统称线性表），栈与线性表的最大区别是数据的存取的操作，我们可以这样认为栈(Stack)是一种特殊的线性表，其插入和删除操作只允许在线性表的一端进行，一般而言，把允许操作的一端称为栈顶(Top)，不可操作的一端称为栈底(Bottom)，同时把插入元素的操作称为入栈(Push),删除元素的操作称为出栈(Pop)。若栈中没有任何元素，则称为空栈，栈的结构如下图： 

 由图我们可看成栈只能从栈顶存取元素，同时先进入的元素反而是后出，而栈顶永远指向栈内最顶部的元素。到此可以给出栈的正式定义：栈(Stack)是一种有序特殊的线性表，只能在表的一端(称为栈顶，top，总是指向栈顶元素)执行插入和删除操作，最后插入的元素将第一个被删除，因此栈也称为后进先出(Last In First Out,LIFO)或先进后出(First In Last Out FILO)的线性表。栈的基本操作创建栈，判空，入栈，出栈，获取栈顶元素等，注意栈不支持对指定位置进行删除，插入，其接口Stack声明如下：

package com.spring.test;

/**
 * 栈接口抽象数据类型
 */
public interface Stack<T> {

    /**
     * 栈是否为空
     * @return
     */
    boolean isEmpty();

    /**
     * data元素入栈
     * @param data
     */
    void push(T data);

    /**
     * 返回栈顶元素,未出栈
     * @return
     */
    T peek();

    /**
     * 出栈,返回栈顶元素,同时从栈中移除该元素
     * @return
     */
    T pop();
}

package com.spring.test;

import java.io.Serializable;
import java.util.EmptyStackException;

/**
 * Created by Administrator on 2018/3/9.
 */
public class SeqStack<T> implements Stack<T>,Serializable {

    private static final long serialVersionUID = -5413303117698554397L;

    /**
     * 栈顶指针,-1代表空栈
     */
    private int top=-1;

    /**
     * 容量大小默认为10
     */
    private int capacity=10;

    /**
     * 存放元素的数组
     */
    private T[] array;

    private int size;

    public SeqStack(int capacity){
        array = (T[]) new Object[capacity];
    }

    public SeqStack(){
        array= (T[]) new Object[this.capacity];
    }

    public  int size(){
        return size;
    }


    @Override
    public boolean isEmpty() {
        return this.top==-1;
    }

    /**
     * 添加元素,从栈顶(数组尾部)插入
     * @param data
     */
    @Override
    public void push(T data) {
        //判断容量是否充足
        if(array.length==size)
            ensureCapacity(size*2+1);//扩容

        //从栈顶添加元素
        array[++top]=data;

        size++;
    }

    /**
     * 获取栈顶元素的值,不删除
     * @return
     */
    @Override
    public T peek() {
        if(isEmpty())
            new EmptyStackException();
        return array[top];
    }

    /**
     * 从栈顶(顺序表尾部)删除
     * @return
     */
    @Override
    public T pop() {
        if(isEmpty()){
            new EmptyStackException();
        }
        size--;
        return array[top--];
    }

    /**
     * 扩容的方法
     * @param capacity
     */
    public void ensureCapacity(int capacity) {
        //如果需要拓展的容量比现在数组的容量还小,则无需扩容
        if (capacity<size){
            return;
        }

        T[] old = array;
        array = (T[]) new Object[capacity];
        //复制元素
        for (int i=0; i<size ; i++){
            array[i]=old[i];
        }
    }

    }

package com.spring.test;

/**
 *
 */
public class EqualsToHashcodeTest {
    public static void main(String[] args) {
        SeqStack<String> s = new SeqStack<String>();
        s.push("a");
        s.push("B");
        s.push("C");
        int l =s.size();
        System.out.println("size-->"+s.size());//size在减少，必须先记录
        for(int i=0;i<l;i++){
            System.out.println("s.pop"+s.pop());
        }
        System.out.println("s.peek-->"+s.peek());

    }
}

链式栈的设计与实现

 了解完顺序栈，我们接着来看看链式栈，所谓的链式栈（Linked Stack），就是采用链式存储结构的栈，由于我们操作的是栈顶一端，因此这里采用单链表（不带头结点）作为基础，直接实现栈的添加，获取，删除等主要操作即可。其操作过程如下图：

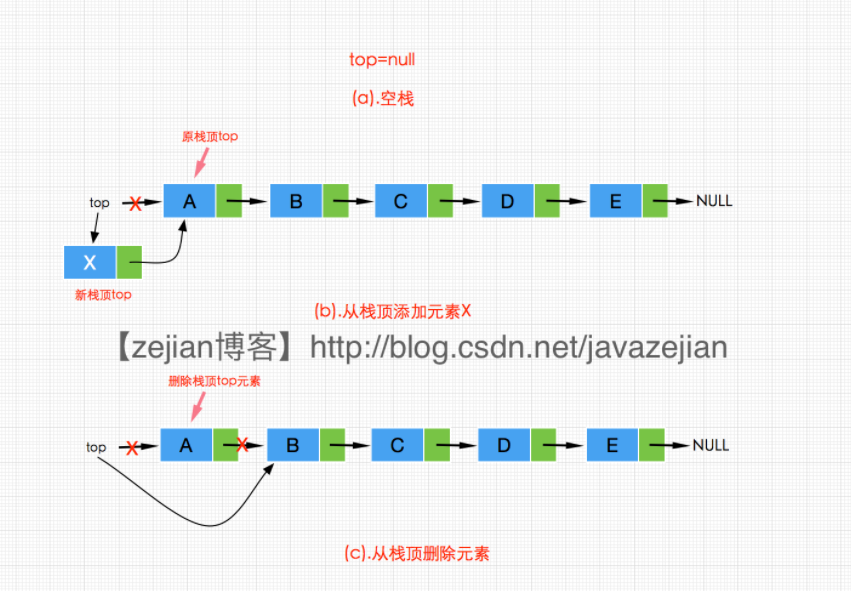
从图可以看出，无论是插入还是删除直接操作的是链表头部也就是栈顶元素，因此我们只需要使用不带头结点的单链表即可。代码实现如下，比较简单，不过多分析了：