tg2015 信息传递 （洛谷p2661)

题目描述

有n个同学（编号为1到n）正在玩一个信息传递的游戏。在游戏里每人都有一个固定的信息传递对象，其中，编号为i的同学的信息传递对象是编号为Ti同学。

游戏开始时，每人都只知道自己的生日。之后每一轮中，所有人会同时将自己当前所知的生日信息告诉各自的信息传递对象（注意：可能有人可以从若干人那里获取信息，但是每人只会把信息告诉一个人，即自己的信息传递对象）。当有人从别人口中得知自己的生日时，游戏结束。请问该游戏一共可以进行几轮？

输入输出格式

输入格式：

输入共2行。

第1行包含1个正整数n表示n个人。

第2行包含n个用空格隔开的正整数T1,T2,……,Tn其中第i个整数Ti示编号为i

的同学的信息传递对象是编号为Ti的同学，Ti≤n且Ti≠i

数据保证游戏一定会结束。

输出格式：

输出共 1 行，包含 1 个整数，表示游戏一共可以进行多少轮。

输入输出样例

输入样例#1：

5
2 4 2 3 1

输出样例#1：

3

说明

样例1解释

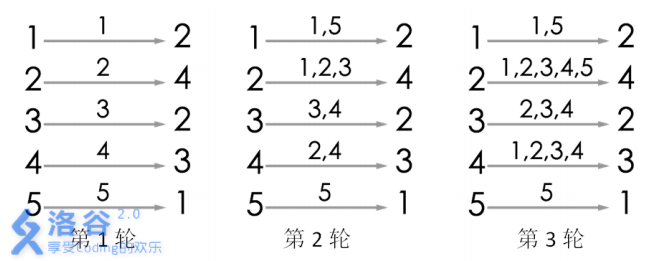
游戏的流程如图所示。当进行完第 3 轮游戏后， 4 号玩家会听到 2 号玩家告诉他自

己的生日，所以答案为 3。当然，第 3 轮游戏后， 2 号玩家、 3 号玩家都能从自己的消息

来源得知自己的生日，同样符合游戏结束的条件。

对于 30%的数据， n ≤ 200；

对于 60%的数据， n ≤ 2500；

对于 100%的数据， n ≤ 200000。

算法：深搜

分析：第一次写炸了，回过头来想一想，发现算法是错误的，这道题正解应该是图论，拓扑排序找最小环，

但深搜也还是很好理解的。（这种思路是借鉴某位大牛的程序才恍然大悟的)

用三个数组，a记边（读入),b记在以哪个枝点为开始的环内，f记此点在环内的步数。

随便取一个点i为环的开端，沿着边走下去，记下步数存入f中，再将b[k]赋成i。

当遇到一个点b[k]不为0时，有两种情况：

1.成为新环，跳出并取小。

2.遇到旧环，特判b[k]<>i那么不计。

 

还有一个问题，怎样算出环的长度？f数组会多出，因为b数组记的不是环，会有另外的点。

设num是b数组内的点数，j是成为新环时判断的点，那么，环长就是num-f[j]

(可以画个图理解一下,毕竟是tg的题，不那么容易想到）

var
 i,j,k,n,m,ans,num:longint;
 a,b,f:array[0..200000+7] of longint;
begin
 read(n);
 for i:=1 to n do read(a[i]);
 fillchar(b,sizeof(b),0);
 fillchar(f,sizeof(f),0);
 ans:=maxlongint;
 for i:=1 to n do
  begin
   if b[i]<>0 then continue;
   k:=i;
   num:=0;
   while b[k]=0 do
    begin
     f[k]:=num;
     inc(num);
     b[k]:=i;
     k:=a[k];
    end;
   if b[k]<>i then continue;
   num:=num-f[k];
   if num<ans then ans:=num;
  end;
 writeln(ans);
end.