这道题神仙到让我面临着买不到冰皮月亮蛋糕的风险来写题解
(蛋糕真好吃呜呜呜)
这篇题解参考了CQzhangyu神仙的做法。
(目测比标程科学好写)
限制是要回文,根据我们做字符串计数的常识,一定是尽量能匹配的先匹配上,这样就不会重复计数了。
因此,可以想到一种直观的DP方法:
令$f[i][j][k]$表示前面匹配到i后面匹配到j加入了k个字符的方案数,我们每次看它是否和前后匹配来转移。
那么它应该是一个有限状态自动机上的转移 大概长这个样子

相当于有向图上路径计数,于是就可以矩乘优化。考虑它有S^3个节点,肯定没戏的。
进一步优化
我们把前后不同的转移标记为红点 它有方案数为24的自环,相同类似的标为绿点。
那么我们发现我们其实并不关心红绿的顺序,我们只关心它出现的次数,最后乘上方案数就可以了。
先考虑我们如何得到这个方案数,用$f[i][j][k]$表示前i个和后j个,走过k个红点的方案数。
有两种转移
1.ch[i]==ch[j]
$f[i+1][j-1][k] += f[i][j][k]$
2.ch[i]!=ch[j]
$f[i+1][j][k]+=f[i][j][k]$
$f[i][j-1][k]+=f[i][j][k]$
我们现在再来看看原来的自动机变成了什么样子
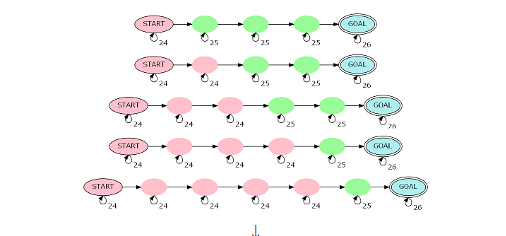
应该是这个样子,每一条链有x个红点 $lceil frac{n-x}{2} ceil$个绿点
如果我们再把它们合并到一张图中,应该长这个样子了
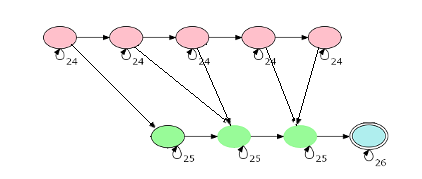
(盗CQzhangyu神仙的图)
我们把方案数直接放到红点与绿点之间的边上。
那么我们就有了一个很科学的解法了,我们现在再在这个图上跑矩乘就ok了。
等等,奇数好像不大对?
我们发现奇数的时候匹配ch[i]和ch[i+1]以后不能直接随便填的转移,它们分别位于中间的两边并且中间的元素填的跟它们一样的时候我们算重了1次,所以方案数多了。
那么我们重新再做一遍类似的矩乘就可以了,现在红点绿点之间的边是强制$ch[i]==ch[i+1]$的方案数。
最后终点还要去掉自环,这样我们的方案数就算对了。
接着你发现你T了!
可以发现我们是个DAG所以按照拓扑序转移可以顺序枚举点,这样加上一个1/6常数就能跑过了qwq
我觉得此题过于神仙QAQ
当然还有更神仙的解法来自cz_xuyixuan巨佬
(讲真我看到这个做法直接惊呆了= =)
还有官方题解的做法,其实就是不缩点而已,个人认为CQzhangyu神仙的解法更为简便。
附代码。

//Love and Freedom. #include<cstdio> #include<algorithm> #include<cstring> #include<cmath> #define ll long long #define inf 20021225 #define mdn 10007 #define N 310 using namespace std; int read() { int s=0,f=1; char ch=getchar(); while(ch<'0'||ch>'9'){if(ch=='-') f=-1; ch=getchar();} while(ch>='0'&&ch<='9') s=s*10+ch-'0',ch=getchar(); return f*s; } struct mat { int a[N][N],n; void init(){memset(a,0,sizeof(a));} void det(){init(); for(int i=0;i<=n;i++) a[i][i]=1;} }s,t; mat operator*(mat a,mat b) // 1/6! { mat tmp; tmp.n=a.n; tmp.init(); for(int i=0;i<=a.n;i++) for(int j=i;j<=a.n;j++) for(int k=i;k<=j;k++) tmp.a[i][j]=(tmp.a[i][j]+a.a[i][k]*b.a[k][j])%mdn; return tmp; } mat ksm(mat bs,int mi,mat &ans) { while(mi) { if(mi&1) ans=ans*bs; bs=bs*bs; mi>>=1; } return ans; } int f[210][210][210],g[210]; char ch[N]; int n,d; void upd(int &x,int y){x+=x+y>=mdn?y-mdn:y;} void dp() { f[1][n][0]=1; for(int i=1;i<=n;i++) for(int j=n;j>=i;j--) if(ch[i]==ch[j]) for(int k=0;k<i+n-j;k++) if(i+1<j) upd(f[i+1][j-1][k],f[i][j][k]); else upd(g[k],f[i][j][k]); else for(int k=0;k<i+n-j;k++) upd(f[i+1][j][k+1],f[i][j][k]), upd(f[i][j-1][k+1],f[i][j][k]); } int main() { scanf("%s",ch+1); n=strlen(ch+1); d=read(); dp(); int top=n+(n+1)/2+1; s.n=t.n=top; s.a[0][1]=1; s.a[0][top-(n+1)/2]=g[0]; t.a[top][top]=26; for(int i=1;i<=n;i++) { t.a[i][i]=24,t.a[i][top-(n-i+1)/2]=g[i]; if(i!=n) t.a[i][i+1]=1; } for(int i=n+1;i<top;i++) t.a[i][i+1]=1,t.a[i][i]=25; if((n+d)&1) { ksm(t,d+n+1>>1,s); int ans=s.a[0][top]; s.init(); t.init(); memset(g,0,sizeof(g)); for(int i=1;i<n;i++) if(ch[i]==ch[i+1]) for(int j=0;j<=n;j++) upd(g[j],f[i][i+1][j]); s.a[0][1]=1; s.a[0][top-(n+1)/2]=g[0]; for(int i=1;i<=n;i++) { t.a[i][i]=24,t.a[i][top-(n-i+1)/2]=g[i]; if(i!=n) t.a[i][i+1]=1; } for(int i=n+1;i<top;i++) t.a[i][i+1]=1,t.a[i][i]=25; ksm(t,d+n+1>>1,s); printf("%d ",(ans-s.a[0][top]+mdn)%mdn); } else ksm(t,d+n>>1,s),printf("%d ",s.a[0][top]); return 0; }
