
基本概念
F(t) - Cumulative Distribution Function (CDF) 积累失效概率函数;
R(t) - Reliability Function 可靠度函数, R(t) = 1 − F(t);
f(t) - Probability Density Function (PDF) 失效概率密度函数,f(t) = dF (t)/dt;
λ(t)/h(t) - Failure (or hazard) rate Function 失效率函数, λ(t) = f(t)/R(t) = f(t)/(1 − F(t) );




A1、二项分布(Binomial)
二项分布 是n个独立的是/非试验中成功的次数的离散概率分布,其中每次试验的成功概率为p;
这样的单次成功/失败试验又称为伯努利试验。二项分布也由伯努利(Bernoulli)提出。
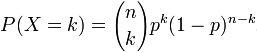 ,
, 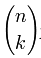 表示
表示 
A2、泊松(Poisson)分布
泊松分布:当 n 很大,p极小时,二项分布的一种近似快速算法。
 , λ = np
, λ = np
二项分布 到 泊松分布的推算。
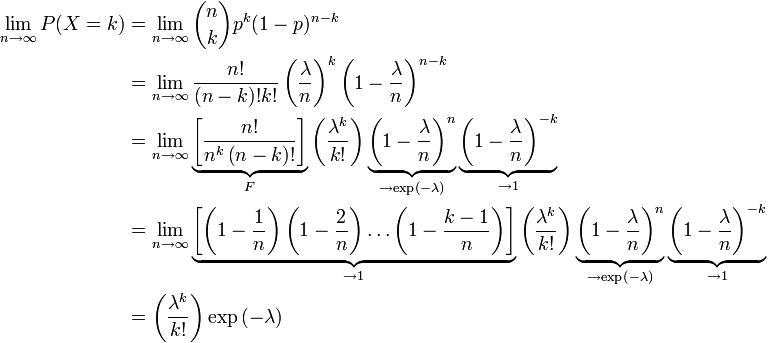
A3、负指数分布
负指数分布又称指数分布。泊松事件流的等待时间(相继两次出现之间的间隔)服从指数分布。

可知,指数分布对应的 h(t) 为 λ(对应泊松分布的 n*p)。常用于描述元件偶然失效期间,固定失效率 λ 下的 失效分析。
另外,常用于假定排队系统中服务器的服务时间和Petri网中变迁的实施速率符合指数分布。
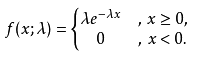


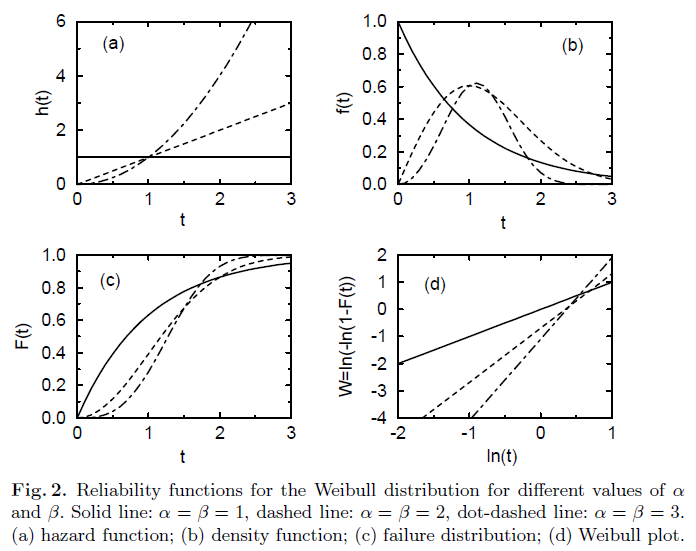
A4、韦布尔(Weibull)分布
α>0是比例参数(scale parameter),也常用 λ 表示;β>0是形状参数(shape parameter),也常用 k 表示。
它的累积分布函数是扩展的指数分布,当β=1,等价于指数分布;β=2时,等价于Rayleigh distribution(瑞利分布)。
威布尔分布在可靠性工程中被广泛应用,被广泛应用于各种寿命试验的数据处理。
β < 1 表示故障率随时间减小。 β = 1 表示故障率恒定。β > 1 表示故障率随时间增加。分别对应 失效浴盆曲线 的 早期失效期、偶然失效期、损耗失效期。

===> ln ( -ln(1-F(t)) ) = βln(t) - ln(α) = β( ln(t) - ln(T63) ).
其中:α = T63^β, T63 对应 F(t=T63) = 0.632 的时刻。
B1、正态分布
B2、![]() Distribution(卡方分布)
Distribution(卡方分布)
若n个相互独立的随机变量ξ₁,ξ₂,...,ξn ,均服从标准正态分布(也称独立同分布于标准正态分布),则这n个服从标准正态分布的随机变量的平方和构成一新的随机变量,其分布规律称为卡方分布(chi-square distribution)。
![]() 分布在数理统计中具有重要意义。
分布在数理统计中具有重要意义。
![]() 分布是由阿贝(Abbe)于1863年首先提出的,后来由海尔墨特(Hermert)和现代统计学的奠基人之一的卡·皮尔逊(C K.Pearson)分别于1875年和1900年推导出来。
分布是由阿贝(Abbe)于1863年首先提出的,后来由海尔墨特(Hermert)和现代统计学的奠基人之一的卡·皮尔逊(C K.Pearson)分别于1875年和1900年推导出来。
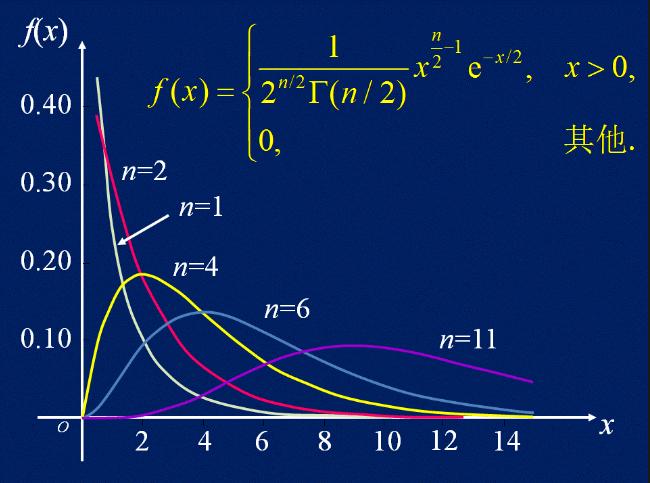
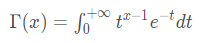
从上图可见当自由度 n 越大,密度曲线越趋于对称,越接近正态分布;n越小, 曲线越不对称。
当 n = 1, 2 时曲线是单调下降趋于 0;当 n ≥ 3时曲线有单峰, 从 0 开始先单调上升, 在一定位置达到峰值, 然后单下降趋向于 0。
卡方分布密度曲线下的面积都是1。查表时为,特定自由度n下,曲线下积分面积的分数位对应的x。例如 n=1, 5%下 x=3.841。
B3、对数正态分布
XX.Student分布(S分布)
【工具软件】
1)PPM Calulator
https://www.maximintegrated.com/en/design/design-tools/calculators/general-engineering/ppm.html
http://www.ti.com/support-quality/reliability/DPPM-sample-size-calculator.html
【参考文档】
1) https://zhuanlan.zhihu.com/c_158803178 【入门】可靠性知道 专栏
2) https://blog.csdn.net/anshuai_aw1/article/details/82735201 【深入】三大抽样分布:卡方分布,t分布和F分布的简单理解
3) https://wenku.baidu.com/view/ab59abb8c77da26925c5b0a3.html 【基础】几种常见的分布
4) https://wenku.baidu.com/view/f5333220a98271fe910ef987.html 【基础】可靠性数学基础
5) https://wenku.baidu.com/view/29fb0cb9a45177232e60a2a5.html 【基础】机械产品的可靠性概率分布
【引用请声明出处,yvivid】https://www.cnblogs.com/yvivid/p/reliability_probability.html