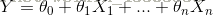Python实现线性回归1，使用解析解求θ

线性回归模型是最简单的机器学习模型，基础可以从线性回归模型开始入手，慢慢地过渡到非线性回归以及神经网络模型。

1.概念

在统计学中，线性回归(Linear Regression)是利用称为线性回归方程的最小平方函数对一个或多个自变量和因变量之间关系进行建模的一种回归分析。这种函数是一个或多个称为回归系数的模型参数的线性组合。只有一个自变量的情况称为简单回归,大于一个自变量情况的叫做多元回归。（这反过来又应当由多个相关的因变量预测的多元线性回归区别，而不是一个单一的标量变量。） 来源：百度百科

2.线性回归

简单回归：最简单的情况，一个自变量输入，Y~X是一对一的关系，映射到几何上来说就是二维坐标系的直线方程，可表示为Y=θX，通过训练得到θ的过程。
多元回归：多个自变量，改变维度的大小。即：

这里的 表示偏移量（或称作截距项），表示空间分布。实际上，Y和θX是一种矩阵形式乘，即，同样从训练中的得到参数 的矩阵向量的过程。

3.最小二乘法 【通过向量运算】

大多情况下都是求近似最优解，即满足估计值于实际值的方差最小时的参数解，可以表示为：
函数模型：

损失函数：

用向量形式书写为：

最小二乘法公式其实就是用欧几里得距离求解空间向量距离，使得所有样本点到估计的回归线段之间的距离和最短，也就是要使损失函数最小，这要对函数进行求导计算，标准方程（标准解析解）：

以下便直接使用这个标准方程直接进行求解（注意：（XTX）^-1，矩阵的逆可能不存在，求解时需要进行判断，存在时才能求解析解θ）

def linearRegLsq(x,y):
    # 最小二乘法直接求解theta
    xtx = np.dot(x.T, x)
    if np.linalg.det(xtx) == 0.0: # 判断xtx行列式是否等于0，奇异矩阵不能求逆
        print('Can not resolve the problem')
        return
    theta_lsq = np.dot(np.dot(np.linalg.inv(np.dot(x.T, x)), x.T), y)
    return theta_lsq

# 2、最小二乘法，直接求解析解θ
    theta_lsq = linearRegLsq(x,y)
    print('')
    print('2、最小二乘法，theta解析解：',theta_lsq.reshape(1,3)[0])

参考资料：
1、python实现线性回归
2、机器学习：线性回归与Python代码实现
3、python实现简单线性回归
4、Machine-Learning-With-Python
5、《机器学习》西瓜书，周志华
6、机器学习视频，邹博
7、 斯坦福大学公开课 ：机器学习课程