归并算法具有稳定性
算法思想:
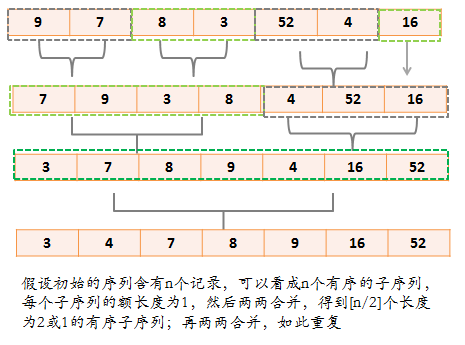
代码:
template <typename Comparable> void mergeSort(vector<Comparable>&a) { mergeSort(a,0,a.size()-1); } template <typename Comparable> void mergeSort(vector<Comparable>&a,int left, int right) { if (left < right) { int mid = (left + right)/2; mergeSort(a,left, mid); mergeSort(a,mid+1,right); merge(a,left, mid+1,right); } } template <typename Comparable> void merge (vector<Comparable>&a, int leftStart, int rightStart, int rightEnd) { int leftEnd = rightStart - 1; int numElements = rightEnd - leftStart + 1; vector<Comparable>temp(numElements); int indexTemp = 0; int tempLeftStart = leftStart; while ( leftStart <= leftEnd && rightStart <= rightEnd ) { if ( a[leftStart] <= a[rightStart] ) temp[indexTemp++] = a[leftStart++]; else temp[indexTemp++] = a[rightStart++]; } while ( leftStart <= leftEnd ) temp[indexTemp++] = a[leftStart++]; while ( rightStart <= rightEnd ) temp[indexTemp++] = a[rightStart++]; for ( int i = 0; i < numElements; ++i ) a[tempLeftStart + i] = temp[i]; }
有稳定性
python版本代码
def merge(data, leftStart, rightStart, rightEnd): leftEnd = rightStart - 1 numElements = rightEnd - leftStart + 1 temp = [] tempLeftStart = leftStart while(leftStart <= leftEnd and rightStart <= rightEnd): if (data[leftStart] <= data[rightStart]): temp.append(data[leftStart]) leftStart += 1 else: temp.append(data[rightStart]) rightStart += 1 while leftStart <= leftEnd: temp.append(data[leftStart]) leftStart += 1 while rightStart <= rightEnd: temp.append(data[rightStart]) rightStart += 1 i = 0 while i < numElements: data[tempLeftStart + i] = temp[i] i += 1 def mergeSort(data, left, right): """归并排序""" if left < right: mid = (left + right) // 2 mergeSort(data, left, mid) mergeSort(data, mid+1, right) merge(data, left, mid+1, right) return data