神经元
想一想便知道,当一个人捏你一下以至于你会痛得叫起来的力度便是神经元的阈值,而我们构建的时候也是把这种现象抽象成一个函数,叫作激活函数。
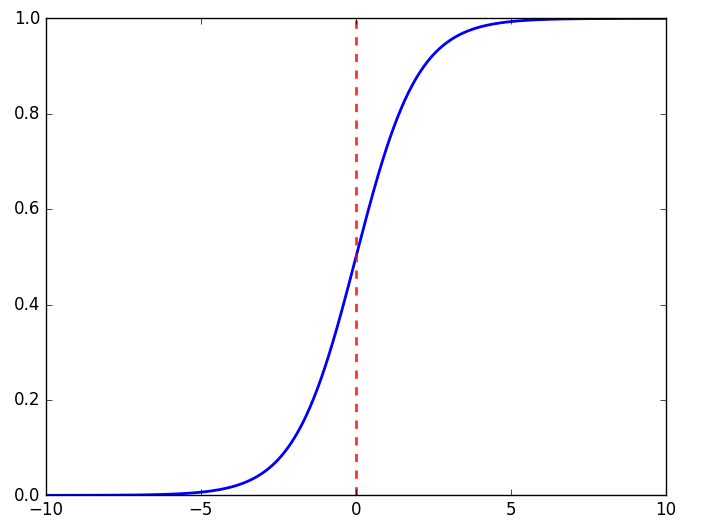
而这里便是我们使用sigmoid函数的原因,它是一个很简单的函数,平滑更接近显示。
$$y=frac{1}{1+e^{-x}}$$
神经网络传递信号
神经网络便是通过一个一个神经元连接,使用权值x输入的和在通过sigmoid函数得到最终的输出值,然后一层一层的传递下去。
其中,(O)为输出矩阵,(W)为权值矩阵,(I)为输入矩阵。
举个栗子:
假设我们设置一个三层神经网络,分别为输入层,隐藏层(注意:不管我们中间有多少层,中间的都叫隐藏层,我们这里隐藏层只有一层),输出层。
1.输入层->隐藏层:我们输入矩阵是一个(3x1)的矩阵,那么我们设置四个权值,那么我们的第一个权值矩阵(就是输入层->隐藏层的)的维度也就为(4x3),这时我们相乘也就得到输出矩阵(4x1),进行下一步时,这个(4x1)的输出矩阵就变成了输入;
2.隐藏层->输出层:这是我们的输入矩阵是一个(4x1)的矩阵,然后我们要求输出层输出为两个值,那么我们第二个权值矩阵(就是隐藏层->输出层的)的维度也就为(2x4),这时我们相乘也就得到输出矩阵(2x1),也就为最终的结果了。
反向传播
现在我们已经可以收到由前面的层传输过来的结果了,但答案肯定是不准的,那么我们该如何进行改进呢?
毫无疑问,首先我们要计算误差,假设真实值为t,输出值为o,那么误差e就为:
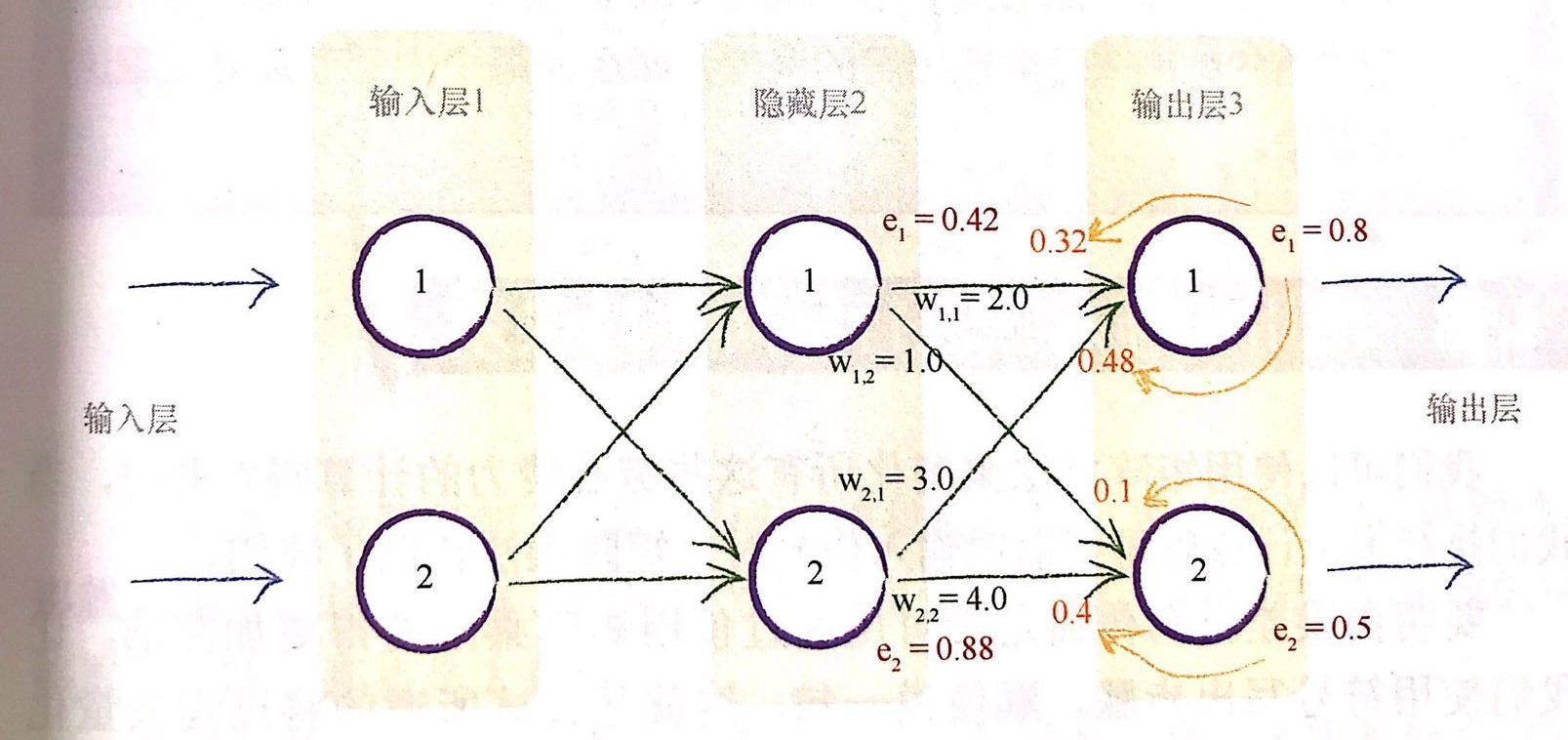
我们按照上图来进行举例说明。
1.更新误差
那么,隐藏层的误差如何确定呢?
我们使用链接(w_{1,1})和链接(w_{2,1})上的分割误差之和来进行更新,也就是
我们也进行带值进行计算
2.使用矩阵进行更新
我们发现上面的公式应用到矩阵运算会很复杂,我们究其本质,最重要的事情是输出误差与链接权重(w_{ij})的乘法。较大的权重就意味着携带较多的输出误差给隐藏层,这些分数的分母是一种归一化因子。如果我们忽略这种因子,那么我们仅仅失去后溃误差的大小。
也就是这里我们使用(e_1*w_{1,1})来代替(e_1*w_{1,1}/(w_{1,1}+w_{2,1})) 。那么我们就可以很容易的进行矩阵运算进行误差更新了。
3.更新权重
在神经网络中,我们采用梯度下降法来寻找最优的权重值。神经网络本身的输出函数部署一个误差函数,但我们知道,由于误差是目标训练值与实际输出值之间的差值,因此我们可以很容易的构建误差函数,即
为什么我们要构建平方项呢?为何不用绝对值误差呢?原因有三
- 使用误差的平方,我们可以很容易的使用代数计算出梯度下降的斜率;
- 误差函数平滑连续,这是的梯度下降法很好地发挥作用,没有间断,也没有突然的跳跃;
- 越接近最小值,梯度越小,这意味着,如果我们使用这个函数调节步长,超调的风险就会变得很小。
现在我们要更新(w_{j,k})的权值,那么来推导一下它的更新公式:
首先有
然后根据链式法则得到:
然后我们对其求偏导:
这样我们就得到了最后的权重更新公式:
其中:
输入与输出
1.输入
我们观察sigmoid函数注意到,当输入值变大,激活函数也就会越来越平坦,权重的改变取决于激活函数的梯度,小梯度也就意味着限制了神经网络的学习能力,这就是所谓的饱和神经网络。因此,我们要尽量保持小的输入。
但有趣的是,当输入信号太小,计算机便会损失精度,所以我们要保持输入范围在0.0~1.0之间,但输入为0的话会将(o_j)设置为0,这样的权重更新表达式就会等于0,从而造成学习能力的丧失,我们需要加上一个小小的偏移,例如0.01,避免输入0带来的麻烦。
2.输出
我们使用激活函数得到的值的范围会被限制在0~1之间,注意:逻辑函数甚至不能取到1.0,只能接近于1.0.数学家们称之为渐进于1.0.
因此,我们需要调整目标值,匹配激活函数的可能输出,常见的使用范围为0.0~1.0之间,但我们是取不到0.0和1.0的,所以这里我们也要进行偏移,例如0.01~0.99.
随机初始权重
和输入输出一样,初始的权重设置也要遵从同样地原则。过大的初始权重会造成大的信号传递给激活函数,导致网络饱和,从而降低学习到更好的权重的能力,因此应该避免大的初始权重值。
我们可以从-1.0~+1.0之间随机均匀地挑选初始权重。而我们也希望初始权重的分布是均匀的,经过数学家们的证明,我们有一个比较好的挑选方式,那就是从均值为0、标准方差等于节点传入链接数量平方根倒数的正态分布中进行采样。
总而言之,我们要禁止将初始权重设定为0或者将初始权重设定为像痛得恒定值,这样会很糟糕。
代码实现
import numpy as np
import scipy.special
import matplotlib.pyplot as plt
# neural network class definition
class NeuralNetwork:
def __init__(self, inputnodes, hiddennodes, outputnodes, learningrate):
# set number of nodes in each input, hidden, output layer
self.inodes = inputnodes
self.hnodes = hiddennodes
self.onodes = outputnodes
# learning rate
self.lr = learningrate
# 初始权重矩阵
self.wih = np.random.normal(0.0, pow(self.hnodes, -0.5), (self.hnodes, self.inodes))
self.who = np.random.normal(0.0, pow(self.onodes, -0.5), (self.onodes, self.hnodes))
# 激活函数
self.activation_function = lambda x: scipy.special.expit(x)
pass
def train(self, inputs_list, targets_list):
# 输入
inputs = np.array(inputs_list, ndmin=2).T
targets = np.array(targets_list, ndmin=2).T
# 隐藏层计算
hidden_inputs = np.dot(self.wih, inputs)
hidden_outputs = self.activation_function(hidden_inputs)
# 输出层计算
final_inputs = np.dot(self.who, hidden_outputs)
final_outputs = self.activation_function(final_inputs)
# 误差计算
output_errors = targets - final_outputs
hidden_errors = np.dot(self.who.T, output_errors)
# 反向传播更新权值
self.who += self.lr * np.dot((output_errors * final_outputs * (1.0 - final_outputs)), np.transpose(hidden_outputs))
self.wih += self.lr * np.dot((hidden_errors * hidden_outputs * (1.0 - hidden_outputs)), np.transpose(inputs))
pass
def query(self, inputs_list):
# 输入
inputs = np.array(inputs_list, ndmin=2).T
# 隐藏层计算
hidden_inputs = np.dot(self.wih, inputs)
hidden_outputs = self.activation_function(hidden_inputs)
# 输出层计算
final_inputs = np.dot(self.who, hidden_outputs)
final_outputs = self.activation_function(final_inputs)
return final_outputs
if __name__ == '__main__':
input_nodes = 784
hidden_nodes = 200
output_nodes = 10
learning_rate = 0.2
nn = NeuralNetwork(input_nodes, hidden_nodes, output_nodes, learning_rate)
# 加载数据
train_data_file = open("./mnist_train.csv", "r")
train_data_list = train_data_file.readlines()
train_data_file.close()
print("数据读取完毕")
# 可视化
# all_values = train_data_list[0].split(',')
# image_array = np.asfarray(all_values[1:]).reshape((28, 28))
# plt.imshow(image_array, cmap="Greys", interpolation='None')
# plt.show()
epochs = 2
for e in range(epochs):
print(" ===== epochs %d ===== " % (e+1))
for record in train_data_list:
all_values = record.split(',')
inputs = (np.asfarray(all_values[1:]) / 255 * 0.99) + 0.01
targets = np.zeros(output_nodes) + 0.01
targets[int(all_values[0])] = 0.99
nn.train(inputs, targets)
# 预测
test_data_file = open("./mnist_test.csv", "r")
test_data_list = test_data_file.readlines()
test_data_file.close()
print(len(test_data_list))
t_num = 0
for line in test_data_list:
all_values = line.split(',')
y = all_values[0]
y_pred = np.argmax(nn.query(np.asfarray(all_values[1:]) / 255 * 0.99 + 0.01))
if int(y) == int(y_pred):
t_num += 1
print(t_num)
print(t_num * 1.0 / len(test_data_list))
这份三层神经网络对mnist手写数据集能达到97%的准确度。