You are given string s. Your task is to determine if the given string s contains two non-overlapping substrings "AB" and "BA" (the substrings can go in any order).
The only line of input contains a string s of length between 1 and 105 consisting of uppercase Latin letters.
Print "YES" (without the quotes), if string s contains two non-overlapping substrings "AB" and "BA", and "NO" otherwise.
ABA
NO
BACFAB
YES
AXBYBXA
NO
In the first sample test, despite the fact that there are substrings "AB" and "BA", their occurrences overlap, so the answer is "NO".
In the second sample test there are the following occurrences of the substrings: BACFAB.
In the third sample test there is no substring "AB" nor substring "BA".
注意细节、比如:ABACAB
#include <iostream> #include <cstring> #include <cstdio> using namespace std; #define N 100010 int main() { char s[N]; char s1[]="AB",s2[]="BA"; while(scanf("%s",s)!=EOF) { bool flag=1; int len=strlen(s); if(len<=3) flag=0; else{ char *p=strstr(s,s1); char *q=strstr(s,s2); if(p==NULL || q==NULL) flag=0; else{ if(strstr(p+2,s2) || strstr(q+2,s1)) ; else flag=0; } } if(!flag) cout<<"NO "; else cout<<"YES "; } return 0; }
You have n problems. You have estimated the difficulty of the i-th one as integer ci. Now you want to prepare a problemset for a contest, using some of the problems you've made.
A problemset for the contest must consist of at least two problems. You think that the total difficulty of the problems of the contest must be at least l and at most r. Also, you think that the difference between difficulties of the easiest and the hardest of the chosen problems must be at least x.
Find the number of ways to choose a problemset for the contest.
The first line contains four integers n, l, r, x (1 ≤ n ≤ 15, 1 ≤ l ≤ r ≤ 109, 1 ≤ x ≤ 106) — the number of problems you have, the minimum and maximum value of total difficulty of the problemset and the minimum difference in difficulty between the hardest problem in the pack and the easiest one, respectively.
The second line contains n integers c1, c2, ..., cn (1 ≤ ci ≤ 106) — the difficulty of each problem.
Print the number of ways to choose a suitable problemset for the contest.
3 5 6 1
1 2 3
2
4 40 50 10
10 20 30 25
2
5 25 35 10
10 10 20 10 20
6
In the first example two sets are suitable, one consisting of the second and third problem, another one consisting of all three problems.
In the second example, two sets of problems are suitable — the set of problems with difficulties 10 and 30 as well as the set of problems with difficulties 20 and 30.
In the third example any set consisting of one problem of difficulty 10 and one problem of difficulty 20 is suitable.
暴力即可
#include <iostream> #include <algorithm> #include <cstdio> #include <cstring> using namespace std; #define INF 1<<30 #define N 50 int ans; int n,l,r,x; int c[N]; void dfs(int id,int sum,int mx,int mi,int num){ if(id>n){ if(sum>=l&&sum<=r&&num>=2&&mx-mi>=x)ans++; return; } dfs(id+1,sum+c[id],max(mx,c[id]),min(mi,c[id]),num+1); dfs(id+1,sum,mx,mi,num); } int main() { ans=0; cin>>n>>l>>r>>x; for(int i=1;i<=n;++i)cin>>c[i]; dfs(1,0,0,INF,0); cout<<ans<<endl; return 0; }

 ', and the arguments and the result of the implication are written as '
', and the arguments and the result of the implication are written as '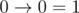

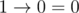
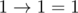
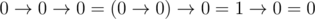 .
.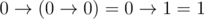 .
. determine if it is possible to place there brackets so that the value of a logical expression is false. If it is possible, your task is to find such an arrangement of brackets.
determine if it is possible to place there brackets so that the value of a logical expression is false. If it is possible, your task is to find such an arrangement of brackets.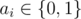 ), which means the values of arguments in the expression in the order they occur.
), which means the values of arguments in the expression in the order they occur.