题目背景
滚粗了的HansBug在收拾旧数学书,然而他发现了什么奇妙的东西。
题目描述
蒟蒻HansBug在一本数学书里面发现了一个神奇的数列,包含N个实数。他想算算这个数列的平均数和方差。
输入输出格式
输入格式:
第一行包含两个正整数N、M,分别表示数列中实数的个数和操作的个数。
第二行包含N个实数,其中第i个实数表示数列的第i项。
接下来M行,每行为一条操作,格式为以下两种之一:
操作13:1 x y k ,表示将第x到第y项每项加上k,k为一实数。
操作2:2 x y ,表示求出第x到第y项这一子数列的平均数。
操作3:3 x y ,表示求出第x到第y项这一子数列的方差。
输出格式:
输出包含若干行,每行为一个实数,即依次为每一次操作2或操作3所得的结果(所有结果四舍五入保留4位小数)。
输入输出样例
输入样例: 输出样例
5 5 3.0000
1 5 4 2 3 2.0000
2 1 4 0.8000
3 1 5
1 1 1 1
1 2 2 -1
3 1 5
说明

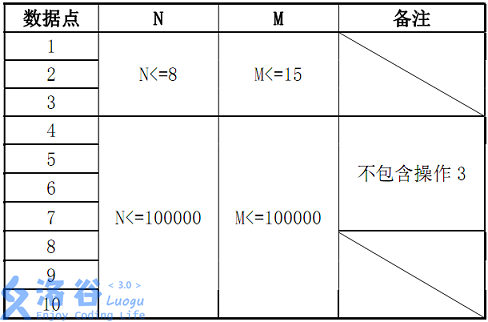
数据范围
-------------------------------------分界线-------------------------------------
题解
这道题要求两个值,一个是平均值,一个是方差,平均值很容易,就是区间和/个数就可以了。但是怎么求方差呢?看上去十分困难,不知道如何下手,不知道怎么维护?但是不妨把方差的公式拆开:
设平均数为k
则S²=[(a1-k)²+(a2-k)²+(a3-k)²+...+(an-k)²]/n(将他拆开)
=[a1²+a2²+a3²+...+an²+nk²-2k(a1+a2+a3+...+an)]/n
∵ (a1+a2+a3+...+an)/n=k
∴ S²=(a1²+a2²+a3²+...+an²)/n-k²
所以现在显而易见要维护方差只要维护平方的和就可以了
那么怎么维护平方和呢?
在拆开一下:
设每个数加上了x
(a1+x)²+(a2+x)²+(a3+x)²+...+(an+x)²
=a1²+a2²+a3²+...+an²+nx²+2x(a1+a2+a3+...+an)
所以现在就很容易了,接下来上代码
#include<cstdio>
#include<cstdlib>
#include<iostream>
using namespace std;
struct node {
double lazy,v,sqr;
} a[400001];
double b[400001];
void pushup(int k) {
a[k].v=a[k<<1].v+a[k<<1|1].v;
a[k].sqr=a[k<<1].sqr+a[k<<1|1].sqr;
}
void add(int k,int l,int r,double v) {
a[k].lazy+=v;
a[k].sqr+=((r-l+1)*v*v+2*v*a[k].v);
a[k].v+=(r-l+1)*v;
}
void pushdown(int k,int l,int r) {
if(a[k].lazy) {
int mid=(l+r)>>1;
add(k<<1,l,mid,a[k].lazy);
add(k<<1|1,mid+1,r,a[k].lazy);
}
a[k].lazy=0;
}
void update(int k,int l,int r,int begin,int end,double c) {
if(r<begin||l>end)
return ;
if(l>=begin&&r<=end) {
add(k,l,r,c);
return;
}
pushdown(k,l,r);
int mid=(l+r)>>1;
update(k<<1,l,mid,begin,end,c);
update(k<<1|1,mid+1,r,begin,end,c);
pushup(k);
}
double find(int k,int l,int r,int begin,int end) {
if(r<begin||l>end)
return 0;
if(l>=begin&&r<=end)
return a[k].v;
pushdown(k,l,r);
int mid=(l+r)>>1;
if(end<=mid)
return find(k<<1,l,mid,begin,end);
else if(begin>mid)
return find(k<<1|1,mid+1,r,begin,end);
else
return find(k<<1,l,mid,begin,mid)+find(k<<1|1,mid+1,r,mid+1,end);
}
double find1(int k,int l,int r,int begin,int end) {
if(r<begin||l>end)
return 0;
if(l>=begin&&r<=end)
return a[k].sqr;
pushdown(k,l,r);
int mid=(l+r)>>1;
if(end<=mid)
return find1(k<<1,l,mid,begin,end);
else if(begin>mid)
return find1(k<<1|1,mid+1,r,begin,end);
else
return find1(k<<1,l,mid,begin,mid)+find1(k<<1|1,mid+1,r,mid+1,end);
}
void build(int k,int l,int r) {
a[k].lazy=0;
if(l==r) {
a[k].v=b[l];
a[k].sqr=b[l]*b[l];
return ;
}
int mid=(l+r)>>1;
build(k<<1,l,mid);
build(k<<1|1,mid+1,r);
pushup(k);
}
int main() {
int n,m,L,x,y;
double c;
scanf("%d%d",&n,&m);
for(int i=1; i<=n; i++)
scanf("%lf",&b[i]);
build(1,1,n);
for(int i=1; i<=m; i++) {
scanf("%d%d%d",&L,&x,&y);
if(L==1) {
scanf("%lf",&c);
update(1,1,n,x,y,c);
}
if(L==2)
printf("%0.4lf
",find(1,1,n,x,y)*1.0/(y-x+1));
if(L==3) {
double ans=find(1,1,n,x,y)*1.0/(y-x+1);
ans*=ans;
printf("%0.4lf
",(find1(1,1,n,x,y)*1.0/(y-x+1))-ans);
}
}
}