斐波那契(Fibonacci)数列的七种实现方法

废话不多说，直接上代码

#include "stdio.h"
#include "queue"
#include "math.h"
using namespace std;

///////////////////////////////////////////////////////////////////////////
//一：递归实现
//	使用公式f[n]=f[n-1]+f[n-2]，依次递归计算，递归结束条件是f[1]=1，f[2]=1。
///////////////////////////////////////////////////////////////////////////
int fib1(int index)     
{
	if(index<1)
	{
		return -1;
	}
	if(index==1 || index==2)
		return 1;
	return fib1(index-1)+fib1(index-2);
}
///////////////////////////////////////////////////////////////////////////
//二：数组实现
//	空间复杂度和时间复杂度都是0(n)，效率一般，比递归来得快。
///////////////////////////////////////////////////////////////////////////
int fib2(int index)
{
	if(index<1)
	{
		return -1;
	}
	if(index<3)
	{
		return 1;
	}
	int *a=new int[index];
	a[0]=a[1]=1;
	for(int i=2;i<index;i++)
		a[i]=a[i-1]+a[i-2];
	int m=a[index-1];
	delete a;         //释放内存空间
	return m;
}
/////////////////////////////////////////////////////////////////////////////
//三：vector<int>实现
//	时间复杂度是0(n)，空间复杂度是0(1)，当然vector有自己的属性会占用资源。
/////////////////////////////////////////////////////////////////////////////
int fib3(int index)           
{
	if(index<1)
	{
		return -1;
	}
	vector<int> a(2,1);      //创建一个含有2个元素都为1的向量
	a.reserve(3);
	for(int i=2;i<index;i++)
	{
		a.insert(a.begin(),a.at(0)+a.at(1));
		a.pop_back();
	}
	return a.at(0);
} 
///////////////////////////////////////////////////////////////////////////////////////////////////////
//四：queue<int>实现
//	当然队列比数组更适合实现斐波那契数列，时间复杂度和空间复杂度和vector<int>一样，但队列太适合这里了，
//	f(n)=f(n-1)+f(n-2)，f(n)只和f(n-1)和f(n-2)有关，f(n)入队列后，f(n-2)就可以出队列了。
///////////////////////////////////////////////////////////////////////////////////////////////////////
int fib4(int index)      
{
	if(index<1)
	{
		return -1;
	}
	queue<int>q;
	q.push(1);
	q.push(1);
	for(int i=2;i<index;i++)
	{
		q.push(q.front()+q.back());
		q.pop();
	}
	return q.back();
}
///////////////////////////////////////////////////////////////////////////////////////////
//五：迭代实现
//	迭代实现是最高效的，时间复杂度是0(n)，空间复杂度是0(1)。
//////////////////////////////////////////////////////////////////////////////////////////
int fib5(int n)          //迭代实现
{
	int i,a=1,b=1,c=1;
	if(n<1)
	{
		return -1;
	}
	for(i=2;i<n;i++)
	{
		c=a+b;     //辗转相加法（类似于求最大公约数的辗转相除法）
		a=b;
		b=c;
	}
	return c;
}
///////////////////////////////////////////////////////////////////////////////////////////////////////
//六：公式实现
//	斐波那契数列有公式的，所以可以使用公式来计算的。
//	由于double类型的精度还不够，所以程序算出来的结果会有误差，如果把公式展开计算，得出的结果就是正确的。
///////////////////////////////////////////////////////////////////////////////////////////////////////
int fib6(int n)
{
	double gh5=sqrt((double)5);
	return (pow((1+gh5),n)-pow((1-gh5),n))/(pow((double)2,n)*gh5);
}

//简单的测试
int main()
{
	printf("%d
",fib1(10));
	printf("%d
",fib2(10));
	printf("%d
",fib3(10));
	printf("%d
",fib4(10));
	printf("%d
",fib5(10));
	printf("%d
",fib6(10));//有误差！
	return 0;
}

七：矩阵乘法

最后一种方法不是一种实用的方法，也比较难以想到，其算法实现也比较复杂，在此单述。

我们将数列写成：

Fibonacci[0] = 0，Fibonacci[1] = 1

Fibonacci[n] = Fibonacci[n-1] + Fibonacci[n-2] (n >= 2)

可以将它写成矩阵乘法形式：

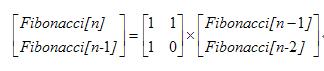
将右边连续的展开就得到：

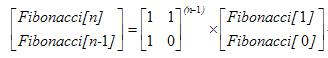
下面就是要用O(log(n))的算法计算：

#include<stdio.h>

struct Matrix2By2
{
	Matrix2By2
		(
		long long m00 = 0, 
		long long m01 = 0, 
		long long m10 = 0, 
		long long m11 = 0
		)
		:m_00(m00), m_01(m01), m_10(m10), m_11(m11) 
	{
	}

	long long m_00;
	long long m_01;
	long long m_10;
	long long m_11;
};

Matrix2By2 MatrixMultiply
	(
	const Matrix2By2& matrix1, 
	const Matrix2By2& matrix2
	)
{
	return Matrix2By2(
		matrix1.m_00 * matrix2.m_00 + matrix1.m_01 * matrix2.m_10,
		matrix1.m_00 * matrix2.m_01 + matrix1.m_01 * matrix2.m_11,
		matrix1.m_10 * matrix2.m_00 + matrix1.m_11 * matrix2.m_10,
		matrix1.m_10 * matrix2.m_01 + matrix1.m_11 * matrix2.m_11);
}

Matrix2By2 MatrixPower(unsigned int n)
{
	Matrix2By2 matrix;
	if(n == 1)
	{
		matrix = Matrix2By2(1, 1, 1, 0);
	}
	else if(n % 2 == 0)
	{
		matrix = MatrixPower(n / 2);
		matrix = MatrixMultiply(matrix, matrix);
	}
	else if(n % 2 == 1)
	{
		matrix = MatrixPower((n - 1) / 2);
		matrix = MatrixMultiply(matrix, matrix);
		matrix = MatrixMultiply(matrix, Matrix2By2(1, 1, 1, 0));
	}

	return matrix;
}

long long fib7(unsigned int n)
{
	int result[2] = {0, 1};
	if(n < 2)
		return result[n];

	Matrix2By2 PowerNMinus2 = MatrixPower(n - 1);
	return PowerNMinus2.m_00;
}

//简单的测试
int main()
{
	printf("%d
",fib7(10));
	return 0;
}