问题
需要情形下,需要将一个区间映射到另一个区间。如将0-1映射到10-32之间,应该如何设计算法?
场景1
比如某大学教师在学校规定的挂科机率下进行期末考试,如果学生都考得很差,那么他就需要根据适当的形式去调整学生的成绩。
比如,学生的成绩普遍较差,分布在20分到65分之间,那么需要映射到55-100之间,将及格率调高。
场景2
某学生是某国交换生,但是在某国的成绩是5-18,但国内的成绩是0-100,需要将国外考试的成绩反映到国内的成绩单上。那么也就是将 5-18 映射到 0-100,将 [5-18] -5 = [0, 13],假设小明的成绩是 12, 那么国内的成绩就是 12*(100/13),原理也就是先归零,然后再同比例缩放 。
原理
假设需要缩放的数据是X,需要映射到的范围是 [a, b], 那么可以用以下公式来进行。
[Y=a+frac{b-a}{X_{max}-X_{min}}.(X-X_{min})
]
代码
def map_rate(X:list, to_min:float, to_max:float)->list:
"""区间映射
Attribute:
- X: 需要映射的列表
- to_min: 要映射到的最小值
- to_max: 要映射到的最大值
"""
x_min=min(X)
x_max=max(X)
return list([round(to_min+((to_max - to_min) / (x_max - x_min)) * i - x_min,1) for i in X])
这个代码比较简单,参数就是上述所提到的三个参数:需要映射的列表, 要映射到的 start 和 end, 最后的结果 round(x, 2)了一下,保留一位小数,否则得到的结果太过精确。
实验
如随机生成的学生成绩=,再将他们映射到某一范围。
X=[67, 45, 81, 95, 23, 77, 65, 32, 55, 22]
map_rate(X, 60, 100)
结果是
[74.7, 62.7, 82.4, 90.1, 50.6, 80.2, 73.6, 55.5, 68.1, 50.1]
分布问题
有点好奇这样是否会影响其分布,推测不会,因为是同比例缩放。于是使用了葡萄牙某中学学生在校成绩数据集,网址是:https://www.mldata.io/dataset-details/school_grades/#customize_download
用上述方法,对数学的成绩分布进行了验证。
data1=pd.read_csv("./学生成绩.csv",encoding='utf8')
with open("./result.csv",'w',encoding='utf8') as f:
result_list="
".join([str(i) for i in map_rate(list(data1['G3']),60,100)])
f.writelines(result_list)
结果如图所示。
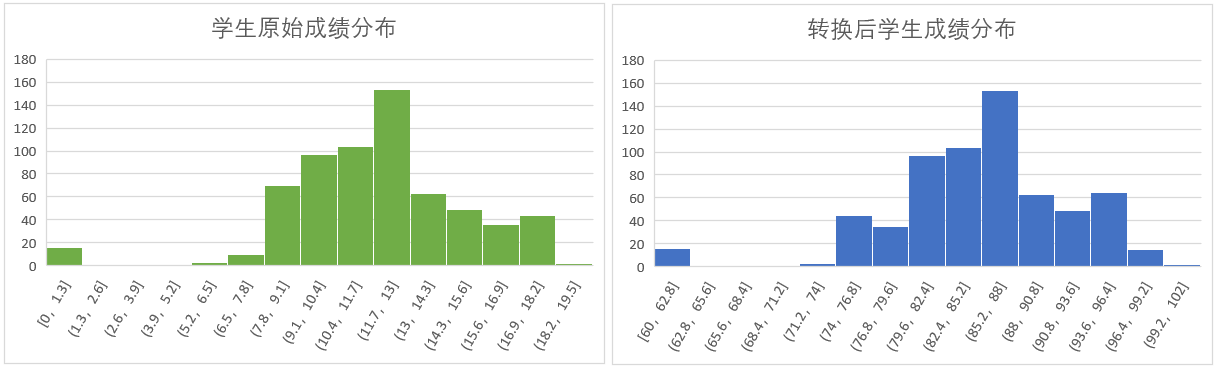
可以看到,基本没有变化,但是会有部分变化,这是因为分布的分箱不同导致的。