用MXNet实现mnist的生成对抗网络(GAN)
生成式对抗网络(Generative Adversarial Network,简称GAN)由一个生成网络与一个判别网络组成。生成网络从潜在空间(latent space)中随机采样作为输入,其输出结果需要尽量模仿训练集中的真实样本。判别网络的输入则为真实样本或生成网络的输出,其目的是将生成网络的输出从真实样本中尽可能分辨出来。而生成网络则要尽可能地欺骗判别网络。两个网络相互对抗、不断调整参数,最终目的是使判别网络无法判断生成网络的输出结果是否真实。从数据的分布来看就是使得生成的数据分布(P_z(z))与原来的数据(P_{data}(x))十分接近,理想的情况下为(P_z(z)=P_{data}(x))。本文给出了GAN的Loss函数、说明GAN的训练原理,再结合最简单的例子mnist,用MXNet来实现GAN。
GAN的基本概念
在一样样本中加入一些精心编制的噪声,会使得原来的分类器失效。图1是一个广为流传的示例,左边的分类器得到的是熊猫而右边被分类为了长臂猿。

为什么会有这样的结果?图像分类器本质上是多维空间中的决策边界,当训练的样本不足时,可能会使得分类器过拟合。当向原样本中加入一些L2范数很小的噪声时,人类的视觉是无法分别这些细微的差别,所以依然会认为和原样本的分类没什么区别。但对过拟合的分类器来说,输入样本的小偏差可能使得最后的决策点越过了原来的决策边界,进入到其它分类中了。这就导致了错误的分类。
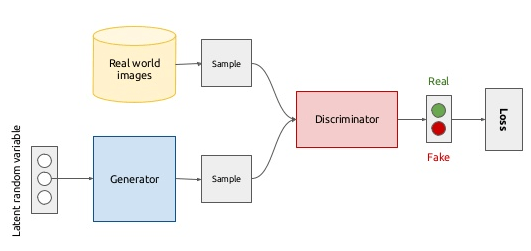
对于生成网络设为G,(G(Z))为生成的对抗样本,理想条件下(G(z))随机生成的样本分布与真实样本分布是一样。对于判别网络设为D,(D(x))为判别样本是真实的概率,理想条件下对真实样本有(G(x)=1),对生成样本有(D(G(z))=0)。为了达到效果,设计了如图2所示的网络结构:
Loss函数如下:
这个Loss函数的优化方法与EM算法的思想是相似的:在G是固定的情况下,判别网络D的精确率越高,那么V就越大;在D固定的条件下,生成网络G的生成的样本越像实际样本,那么V就越小。所有V(G,D)进行了极小极大化博弈:
实现mnist的GAN
MXNet的源码给出了mnsit的GAN实现(见dcgan.py),但是没有给出详细的说明,我在这里详细解释下,源文件在装了相关的python包之后是能正确运行的。DCGAN是指Deep Convolution Generative Adversarial Netword(深度卷积生成式对抗网格)。
mnist的网络相对来说比较简单,如图所示:
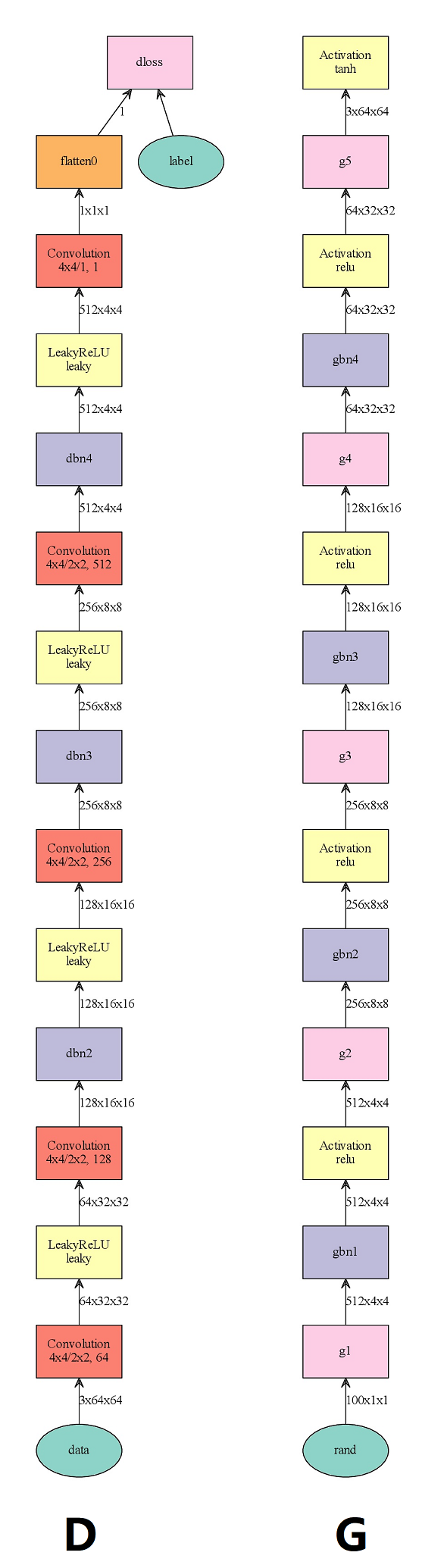
生成网络G的结构与判别网络D的结果是反向对称的(虽然两个网络的开头或者结尾有所不同,但这是为了与结果相对应),这里有一个很重要但被很多文章忽略的假设:判别网络从潜在空间(latent space)是可逆的。不是说从最后的结果是可逆的,但从原始图片映射到潜在空间这个过程(比如说从全连接层的n(n一般比较大)维向量)是可逆的,这里说的可逆不是严格意义上的反函数,而是从视觉判别结果上区别不大,比如说在G与D理想的情况下数字9通过判别网络得到一个100维的向量,再将这个100维向量通过生成网络G得到一张图片,这张图片在人类看来也是9。
代码实现如下:
def make_dcgan_sym(ngf, ndf, nc, no_bias=True, fix_gamma=True, eps=1e-5 + 1e-12):
BatchNorm = mx.sym.BatchNorm
# 生成网络G
# 输入生成网络G的变量,这个是潜在空间
rand = mx.sym.Variable('rand')
g1 = mx.sym.Deconvolution(rand, name='g1', kernel=(4,4), num_filter=ngf*8, no_bias=no_bias)
gbn1 = BatchNorm(g1, name='gbn1', fix_gamma=fix_gamma, eps=eps)
gact1 = mx.sym.Activation(gbn1, name='gact1', act_type='relu')
g2 = mx.sym.Deconvolution(gact1, name='g2', kernel=(4,4), stride=(2,2), pad=(1,1), num_filter=ngf*4, no_bias=no_bias)
gbn2 = BatchNorm(g2, name='gbn2', fix_gamma=fix_gamma, eps=eps)
gact2 = mx.sym.Activation(gbn2, name='gact2', act_type='relu')
g3 = mx.sym.Deconvolution(gact2, name='g3', kernel=(4,4), stride=(2,2), pad=(1,1), num_filter=ngf*2, no_bias=no_bias)
gbn3 = BatchNorm(g3, name='gbn3', fix_gamma=fix_gamma, eps=eps)
gact3 = mx.sym.Activation(gbn3, name='gact3', act_type='relu')
g4 = mx.sym.Deconvolution(gact3, name='g4', kernel=(4,4), stride=(2,2), pad=(1,1), num_filter=ngf, no_bias=no_bias)
gbn4 = BatchNorm(g4, name='gbn4', fix_gamma=fix_gamma, eps=eps)
gact4 = mx.sym.Activation(gbn4, name='gact4', act_type='relu')
g5 = mx.sym.Deconvolution(gact4, name='g5', kernel=(4,4), stride=(2,2), pad=(1,1), num_filter=nc, no_bias=no_bias)
# 生成网络G最后得到一张相片
gout = mx.sym.Activation(g5, name='gact5', act_type='tanh')
# 判别网络D,这里里的结构与一般的分类网络区别不大
data = mx.sym.Variable('data')
label = mx.sym.Variable('label')
d1 = mx.sym.Convolution(data, name='d1', kernel=(4,4), stride=(2,2), pad=(1,1), num_filter=ndf, no_bias=no_bias)
dact1 = mx.sym.LeakyReLU(d1, name='dact1', act_type='leaky', slope=0.2)
d2 = mx.sym.Convolution(dact1, name='d2', kernel=(4,4), stride=(2,2), pad=(1,1), num_filter=ndf*2, no_bias=no_bias)
dbn2 = BatchNorm(d2, name='dbn2', fix_gamma=fix_gamma, eps=eps)
dact2 = mx.sym.LeakyReLU(dbn2, name='dact2', act_type='leaky', slope=0.2)
d3 = mx.sym.Convolution(dact2, name='d3', kernel=(4,4), stride=(2,2), pad=(1,1), num_filter=ndf*4, no_bias=no_bias)
dbn3 = BatchNorm(d3, name='dbn3', fix_gamma=fix_gamma, eps=eps)
dact3 = mx.sym.LeakyReLU(dbn3, name='dact3', act_type='leaky', slope=0.2)
d4 = mx.sym.Convolution(dact3, name='d4', kernel=(4,4), stride=(2,2), pad=(1,1), num_filter=ndf*8, no_bias=no_bias)
dbn4 = BatchNorm(d4, name='dbn4', fix_gamma=fix_gamma, eps=eps)
dact4 = mx.sym.LeakyReLU(dbn4, name='dact4', act_type='leaky', slope=0.2)
d5 = mx.sym.Convolution(dact4, name='d5', kernel=(4,4), num_filter=1, no_bias=no_bias)
d5 = mx.sym.Flatten(d5)
# 用逻辑回归计算最后的loss
dloss = mx.sym.LogisticRegressionOutput(data=d5, label=label, name='dloss')
# 返回这G与D这两个网络
return gout, dloss
在训练的过程中,所有的原样本的label为1,生成网络G生成的样本的label为0,用这样来区别原样本与生成的对抗样本。生成网络输入的潜在空间样本是100维的,训练过程如下:
- 用生成网络G生成对抗样本gout
- 对抗样本的label设为0,因为要先用这个训练判别网络D
- 用gout来训练判别网络D,得到梯度,但不更新
- 对原样本的label设为1,再用之来训练判别网络D
- 得到梯度后合入gout得到的梯度,更新D的参数
- 下面的过程是为了得到生成网络G的loss
- 设gout的label为1,因为生成网络G的目标就是要生成label为1的样本,所以训练G的label为1。反之,如果训练D,为了区别原样本与生成样本所以label为0。
- 用判别网络D来得输入的梯度dgout,这个梯度就是生成网络G的loss。
- 用这个loss反向传播生成网络G,并更新参数。
这里面的关键就是用判别网络D来得到生成网络G的loss,之所以可以这样,是因为这两个网络是可逆的。训练的代码如下:
if __name__ == '__main__':
logging.basicConfig(level=logging.DEBUG)
# =============setting============
dataset = 'mnist'
imgnet_path = './train.rec'
ndf = 64
ngf = 64
nc = 3
batch_size = 64
Z = 100
lr = 0.0002
beta1 = 0.5
ctx = mx.gpu(0)
check_point = False
symG, symD = make_dcgan_sym(ngf, ndf, nc)
#mx.viz.plot_network(symG, shape={'rand': (batch_size, 100, 1, 1)}).view()
#mx.viz.plot_network(symD, shape={'data': (batch_size, nc, 64, 64)}).view()
# ==============data==============
if dataset == 'mnist':
X_train, X_test = get_mnist()
train_iter = mx.io.NDArrayIter(X_train, batch_size=batch_size)
elif dataset == 'imagenet':
train_iter = ImagenetIter(imgnet_path, batch_size, (3, 64, 64))
rand_iter = RandIter(batch_size, Z)
label = mx.nd.zeros((batch_size,), ctx=ctx)
# =============module G=============
modG = mx.mod.Module(symbol=symG, data_names=('rand',), label_names=None, context=ctx)
modG.bind(data_shapes=rand_iter.provide_data)
modG.init_params(initializer=mx.init.Normal(0.02))
modG.init_optimizer(
optimizer='adam',
optimizer_params={
'learning_rate': lr,
'wd': 0.,
'beta1': beta1,
})
mods = [modG]
# =============module D=============
modD = mx.mod.Module(symbol=symD, data_names=('data',), label_names=('label',), context=ctx)
modD.bind(data_shapes=train_iter.provide_data,
label_shapes=[('label', (batch_size,))],
inputs_need_grad=True)
modD.init_params(initializer=mx.init.Normal(0.02))
modD.init_optimizer(
optimizer='adam',
optimizer_params={
'learning_rate': lr,
'wd': 0.,
'beta1': beta1,
})
mods.append(modD)
# ============printing==============
def norm_stat(d):
return mx.nd.norm(d)/np.sqrt(d.size)
mon = mx.mon.Monitor(10, norm_stat, pattern=".*output|d1_backward_data", sort=True)
mon = None
if mon is not None:
for mod in mods:
pass
def facc(label, pred):
pred = pred.ravel()
label = label.ravel()
return ((pred > 0.5) == label).mean()
def fentropy(label, pred):
pred = pred.ravel()
label = label.ravel()
return -(label*np.log(pred+1e-12) + (1.-label)*np.log(1.-pred+1e-12)).mean()
mG = mx.metric.CustomMetric(fentropy)
mD = mx.metric.CustomMetric(fentropy)
mACC = mx.metric.CustomMetric(facc)
print('Training...')
stamp = datetime.now().strftime('%Y_%m_%d-%H_%M')
# =============train===============
for epoch in range(100):
train_iter.reset()
for t, batch in enumerate(train_iter):
rbatch = rand_iter.next()
if mon is not None:
mon.tic()
# 首先生成对抗样本
modG.forward(rbatch, is_train=True)
outG = modG.get_outputs()
# update discriminator on fake
# 这里的负样本label为0,正样本label为1,不像普遍的mnist一样。那么modG就想生成样本label为1的,modD要将modG生成的数据判定为0
# train_iter(真实样本)中的数据判定为1。
label[:] = 0
modD.forward(mx.io.DataBatch(outG, [label]), is_train=True)
modD.backward()
#modD.update()
# 先Copy得到的对抗样本的梯度,要注意是复制不是引用。
gradD = [[grad.copyto(grad.context) for grad in grads] for grads in modD._exec_group.grad_arrays]
modD.update_metric(mD, [label])
modD.update_metric(mACC, [label])
# update discriminator on real
# 对真实样本的数据训练
label[:] = 1
batch.label = [label]
modD.forward(batch, is_train=True)
modD.backward()
# 对抗样本与真实样本的梯度合到一起建行梯度更新
for gradsr, gradsf in zip(modD._exec_group.grad_arrays, gradD):
for gradr, gradf in zip(gradsr, gradsf):
gradr += gradf
modD.update()
modD.update_metric(mD, [label])
modD.update_metric(mACC, [label])
# update generator
# 更新modG的参数,这里要注意的是,modG想要生成的样本label是1的,所以在modD中用了这个label,就是想生成的样本向label=1靠近。
# 前向和向后生成输入数据的梯度diffD
label[:] = 1
modD.forward(mx.io.DataBatch(outG, [label]), is_train=True)
modD.backward()
diffD = modD.get_input_grads()
# diffD就是modG的loss产生的梯度,用它来向后传播并更新参数。
modG.backward(diffD)
modG.update()
mG.update([label], modD.get_outputs())
if mon is not None:
mon.toc_print()
t += 1
if t % 10 == 0:
print('epoch:', epoch, 'iter:', t, 'metric:', mACC.get(), mG.get(), mD.get())
mACC.reset()
mG.reset()
mD.reset()
visual('gout', outG[0].asnumpy())
diff = diffD[0].asnumpy()
diff = (diff - diff.mean())/diff.std()
visual('diff', diff)
visual('data', batch.data[0].asnumpy())
if check_point:
print('Saving...')
modG.save_params('%s_G_%s-%04d.params'%(dataset, stamp, epoch))
modD.save_params('%s_D_%s-%04d.params'%(dataset, stamp, epoch))
训练的结果部分结果如下,gout是生成的样本,data是原样本,diff是它们的差。可以从后面生成的gout中看到,结果缺少一些数字,比如2、3等,这是因为我们没有对各个数字的潜在空间进行生成样本而是用统一的空间,这个统一的空间中对应的数字可能没有2、3等或者说它们点的比例相对来说比较小,样例用到的空间只是保证生成样本是数字,但并不保证每个数字都会有,如果我保证生成每个数字的样本,那么得重新设计程序,但原理和例程相差不大。

过程打印的输出如下:
epoch: 99 iter: 930 metric: ('facc', 1.0) ('fentropy', 8.3449375152587884) ('fentropy', 0.00077932097192388026)
【防止爬虫转载而导致的格式问题——链接】:
http://www.cnblogs.com/heguanyou/p/7642608.html