Java课程课后作业190315之最大连续子数组（二维数组版）

，，　　在本周的课堂上，老师再一次提高了要求，将一维数组升级成为了二维数组，然后求出块状的连续子数组。

　　一开始还想着借鉴之前球一维数组的O（n）的算法，后来还是没有找到头绪，舍友讲了自己的办法，但是没有去仔细去问，也就不了了之，他的那个虽然是O（n四次方）的算法，但是好在实现起来比较简便一点。

　　后来想了想没有想出来，查看相关的资料，找到了和之前求一维数组类似的方法，就是直接将这个二维数组降维，将它压缩成一维数组，这样讲可能不太好理解，下面举一个例子，来阐释这个方法：

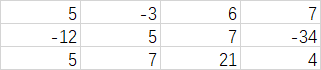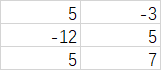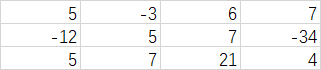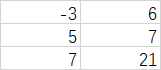　　我们首先设置一个数组：，在这种情况下，我可以将它看成一个一维数组，然后求出它的最大子数组，在这种情况下，则需要将，，，看成三个一维数组中的元素，然后求出它们的最大子数组。依次类推，我们可以求出剩下的情况，，，等。

　　既然知道了怎么做，那么剩下的就是通过遍历来算出所有额最大值，并将他们放入到数组中，然后再通过一次遍历来获得最大的块状连续子数组即可。

public class Main {
    static int length=0;//长度是指这个块状的长度（所占的列数
    static int max_i=0;
    static int line=3;
    static int list=4;
    static int start=0;//start是指开始的列数，即从第几列开始形成块状数组
    static int sumList=(int) (list*(list+1)*0.5);//设置一个储存所有最大子数组的数组
    static int []maxsum=new int[sumList];
private static void max(int p[][]) {
    int remaining=list-start;
    int max = 0;
    int tempsum=0;
    for(int z=0;z<remaining;z++) {
        for(int j=0;j<line;j++) {
            if(length<1) {//这个是只有一列时候的特殊情况
                tempsum=tempsum+p[j][start];
                if(j==0)
                    max=tempsum;
                if(tempsum>max) {
                    max=tempsum;
                }
                if(tempsum<0){
                    tempsum=0;
                }
            }else {
                for(int i=start;i<(length+1+start);i++) {
                    if(i>(list-1)) {
                        break;
                    }
                    tempsum=tempsum+p[j][i];
                    if(j==0)
                        max=tempsum;
                    if(tempsum>max) {
                        max=tempsum;
                    }
                    if(i>=(length+start)) {
                        if(tempsum<0){
                            tempsum=0;
                        }
                    }
                }
            }
        }
        length++;
        maxsum[max_i]=max;
        max_i++;
        tempsum=0;
    }
        start++;
        length=0;
}
private static int MAX(int max[]) {

     System.out.println("输出最大值数组:");
     for(int i=0;i<max.length;i++){
         System.out.print(max[i]+"	");
     }     
     int max_=0;
     for(int i=0;i<max.length;i++){
         if(max[i]>max_){      //求出最大值
             max_=max[i];
         }
     }
     System.out.println("
最大值:"+max_);    
    return 0;
    
}
    public static void main(String[] args) {
        // TODO Auto-generated method stub
        int[][] p= {{5,-3,6,7},
                    {-12,5,7,-34},
                    {5,7,21,4}};//设置一个数组
            for(int i=0;i<list;i++) {
                max(p);    
            }
            MAX(maxsum);

    }

}