已知矩阵A和矩阵B,求A和B的乘积C=AB
矩阵A大小为mxn,矩阵B大小为nxp。

常规方法
矩阵C中每一个元素Cij = A的第i行 乘以(点乘) B的第j列
列方法
矩阵C的第i列 = 矩阵A乘以矩阵B的第i列
注:矩阵A乘以一个向量,相当于对矩阵A的列进行线性组合
行方法
矩阵C的第i行 = 矩阵A的第i行乘以矩阵B
注:矩阵C的每一行是矩阵B的每行的线性组合
列x行
矩阵A的每一列的大小为m x 1,矩阵B的每一行大小为1 x p。
矩阵C=∑矩阵A第i列乘以矩阵B第i行
举例:
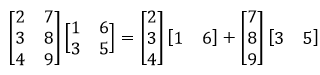
分块乘法法则
比如将矩阵A和矩阵B都分为2x2,则

其实就是把矩阵中每个块看出是一个元素,方法与常规方法一样。