一、L0范数、L1范数、参数稀疏
L0范数是指向量中非0的元素的个数。如果我们用L0范数来规则化一个参数矩阵W的话,就是希望W的大部分元素都是0,换句话说,让参数W是稀疏的。总结:L1范数和L0范数可以实现稀疏,L1因具有比L0更好的优化求解特性而被广泛应用。
参数稀疏的优点,
1)特征选择(Feature Selection):
大家对稀疏规则化趋之若鹜的一个关键原因在于它能实现特征的自动选择。一般来说,xi的大部分元素(也就是特征)都是和最终的输出yi没有关系或者不提供任何信息的,在最小化目标函数的时候考虑xi这些额外的特征,虽然可以获得更小的训练误差,但在预测新的样本时,这些没用的信息反而会被考虑,从而干扰了对正确yi的预测。稀疏规则化算子的引入就是为了完成特征自动选择的光荣使命,它会学习地去掉这些没有信息的特征,也就是把这些特征对应的权重置为0。
2)可解释性(Interpretability):
另一个青睐于稀疏的理由是,模型更容易解释。例如患某种病的概率是y,然后我们收集到的数据x是1000维的,也就是我们需要寻找这1000种因素到底是怎么影响患上这种病的概率的。假设我们这个是个回归模型:y=w1*x1+w2*x2+…+w1000*x1000+b(当然了,为了让y限定在[0,1]的范围,一般还得加个Logistic函数)。通过学习,如果最后学习到的w*就只有很少的非零元素,例如只有5个非零的wi,那么我们就有理由相信,这些对应的特征在患病分析上面提供的信息是巨大的,决策性的。也就是说,患不患这种病只和这5个因素有关,那医生就好分析多了。但如果1000个wi都非0,医生不得不面对这1000种因素。
二、L1范数、L2范数
L2范数的规则项||W||2最小,可以使得W的每个元素都很小,都接近于0,但与L1范数不同,它不会让它等于0,而是接近于0。
L2范数的好处如下,
1)学习理论的角度:
从学习理论的角度来说,L2范数可以防止过拟合,提升模型的泛化能力。
2)优化计算的角度:
从优化或者数值计算的角度来说,L2范数有助于处理 condition number不好的情况下矩阵求逆很困难的问题。
病态条件:
咱们先看左边的那个,第一行假设是我们的AX=b,第二行我们稍微改变下b,得到的x和没改变前的差别很大。第三行我们稍微改变下系数矩阵A,可以看到结果的变化也很大。换句话来说,这个系统的解对系数矩阵A或者b太敏感了。
因为一般我们的系数矩阵A和b是从实验数据里面估计得到的,所以它是存在误差的,如果我们的系统对这个误差是可以容忍的还好,但系统对这个误差太敏感了,我们的解的误差更大,所以这个方程组系统就是ill-conditioned病态的。
右边那个就叫well-condition的系统了。
condition number:
如果方阵A是非奇异的,那么A的 condition number 定义为:
κ(A)=∥A∥∥A−1∥κ(A)=∥A∥∥A−1∥如果方阵 A 是奇异的,那么 A 的 condition number 就是正无穷大了,实际上,每一个可逆方阵都存在一个 condition number。
对condition number来个一句话总结:condition number 是一个矩阵(或者它所描述的线性系统)的稳定性或者敏感度的度量,如果一个矩阵的 condition number 在1附近,那么它就是well-conditioned的,如果远大于1,那么它就是 ill-conditioned 的。
总结:L2范数不但可以防止过拟合,还可以让我们的优化求解变得稳定和快速。
L1和L2的差别,
1)下降速度:
我们知道,L1和L2都是规则化的方式,我们将权值参数以L1或者L2的方式放到代价函数里面去。然后模型就会尝试去最小化这些权值参数。而这个最小化就像一个下坡的过程,L1和L2的差别就在于这个“坡”不同,如下图:L1就是按绝对值函数的“坡”下降的,而L2是按二次函数的“坡”下降。所以实际上在0附近,L1的下降速度比L2的下降速度要快,会非常快得降到0。
2)模型空间的限制:
实际上,对于L1和L2规则化的代价函数来说,我们可以写成以下形式:
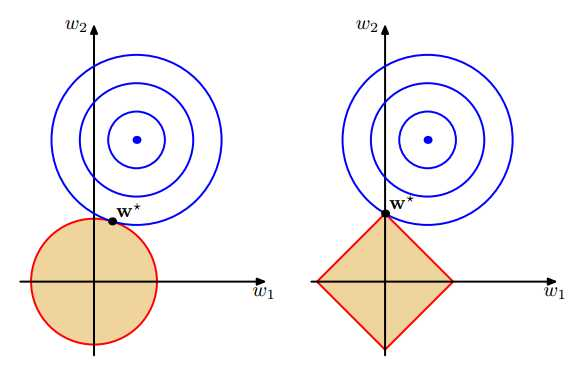
也就是说,我们将模型空间限制在w的一个L1-ball 中。为了便于可视化,我们考虑两维的情况,在(w1, w2)平面上可以画出目标函数的等高线,而约束条件则成为平面上半径为C的一个 norm ball 。等高线与 norm ball 首次相交的地方就是最优解:
可以看到,L1-ball 与L2-ball 的不同就在于L1在和每个坐标轴相交的地方都有“角”出现,而目标函数的测地线除非位置摆得非常好,大部分时候都会在角的地方相交。注意到在角的位置就会产生稀疏性,例如图中的相交点就有w1=0,而更高维的时候(想象一下三维的L1-ball 是什么样的?)除了角点以外,还有很多边的轮廓也是既有很大的概率成为第一次相交的地方,又会产生稀疏性。
相比之下,L2-ball 就没有这样的性质,因为没有角,所以第一次相交的地方出现在具有稀疏性的位置的概率就变得非常小了。这就从直观上来解释了为什么L1-regularization 能产生稀疏性,而L2-regularization 不行的原因了。
总结:L1会趋向于产生少量的特征,而其他的特征都是0,而L2会选择更多的特征,这些特征都会接近于0。Lasso在特征选择时候非常有用,而Ridge就只是一种规则化而已。
有关上面配图的解释:
首先,我们要优化的是这个问题
。
其次,
和
这个优化问题是等价的,即对一个特定的
总存在一个
使得这两个问题是等价的(这个是优化里的知识)。
最后,下面这个图表达的其实
这个优化问题,把
的解限制在黄色区域内,同时使得经验损失尽可能小。
直观来讲:用梯度下降的方法,当w小于1的时候,L2正则项的惩罚效果越来越小,L1正则项惩罚效果依然很大,L1可以惩罚到0,而L2很难。
三、先验知识角度理解L1和L2正则化与参数稀疏
链接:https://www.zhihu.com/question/37096933/answer/70668476
来源:知乎
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
L1,L2范式来自于对数据的先验知识.如果你认为,你现有的数据来自于高斯分布,那么就应该在代价函数中加入数据先验P(x),一般由于推导和计算方便会加入对数似然,也就是log(P(x)),然后再去优化,这样最终的结果是,由于你的模型参数考虑了数据先验,模型效果当然就更好.
哦对了,如果你去看看高斯分布的概率密度函数P(x),你会发现取对数后的log(P(x))就剩下一个平方项了,这就是L2范式的由来--高斯先验.
同样,如果你认为你的数据是稀疏的,不妨就认为它来自某种laplace分布.不知你是否见过laplace分布的概率密度函数,我贴出一张维基上的图,
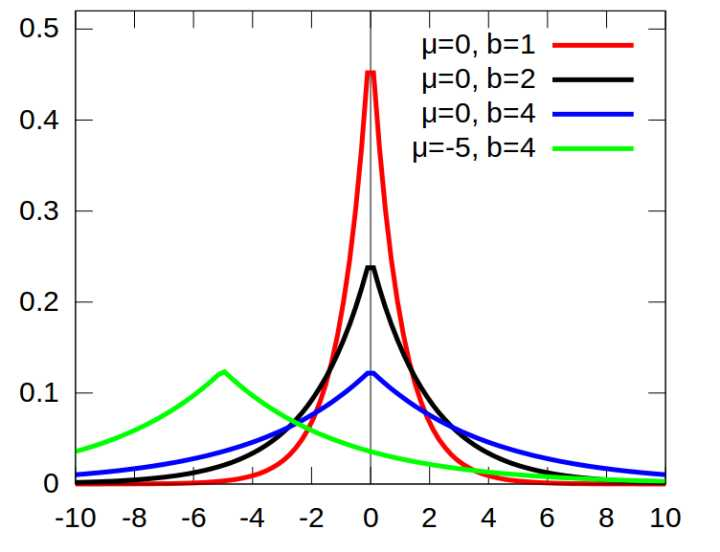
laplace分布是尖尖的分布,是不是很像一个pulse?从这张图上,你应该就能看出,服从laplace分布的数据就是稀疏的了(只有很小的概率有值,大部分概率值都很小或为0).
那么,加入了laplace先验作为正则项的代价函数是什么?
再看看laplace分布的概率密度函数(还是来自维基百科),
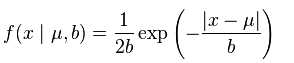
所以用L1范式去正则,就假定了你的数据是laplace分布,是稀疏的.
四、数值计算角度理解L1和L2正则化与参数稀疏
作者:王赟 Maigo链接:https://www.zhihu.com/question/37096933/answer/70426653
来源:知乎
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
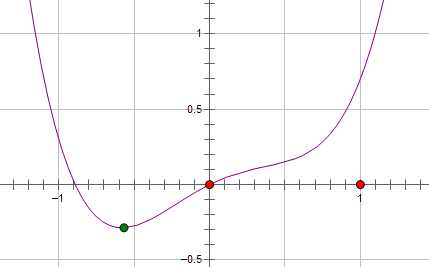
现在施加 L2 regularization,新的费用函数()如图中蓝线所示:
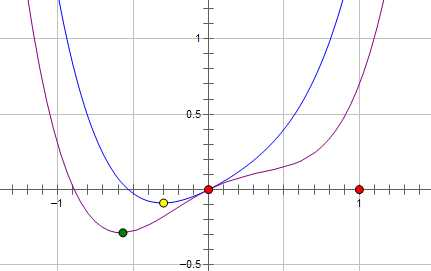
而如果施加 L1 regularization,则新的费用函数()如图中粉线所示:

两种 regularization 能不能把最优的 x 变成 0,取决于原先的费用函数在 0 点处的导数。
如果本来导数不为 0,那么施加 L2 regularization 后导数依然不为 0,最优的 x 也不会变成 0。
而施加 L1 regularization 时,只要 regularization 项的系数 C 大于原先费用函数在 0 点处的导数的绝对值,x = 0 就会变成一个极小值点。