---------------------------------------------------------------------------------------
本系列文章为《机器学习实战》学习笔记,内容整理自书本,网络以及自己的理解,如有错误欢迎指正。
源码在Python3.5上测试均通过,代码及数据 --> https://github.com/Wellat/MLaction
---------------------------------------------------------------------------------------
1 算法概述
1.1 算法特点
简单地说,k-近邻算法采用测量不同特征值之间的距离方法进行分类。
优点:精度高、对异常值不敏感、无数据输入假定
缺点:计算复杂度高、空间复杂度高
适用数据范围:数值型和标称型
1.2 工作原理
存在一个训练样本集,并且每个样本都存在标签(有监督学习)。输入没有标签的新样本数据后,将新数据的每个特征与样本集中数据对应的特征进行比较,然后算法提取出与样本集中特征最相似的数据(最近邻)的分类标签。一般来说,我们只选择样本数据集中前k个最相似的数据,这就是k-近邻算法中k的出处,而且k通常不大于20。最后选择k个最相似数据中出现次数最多的分类,作为新数据的分类。
1.3 实例解释
以电影分类为例子,使用k-近邻算法分类爱情片和动作片。有人曾经统计过很多电影的打斗镜头和接吻镜头,下图显示了6部电影的打斗和接吻镜头数。 假如有一部未看过的电影,如何确定它是爱情片还是动作片呢?

①首先需要统计这个未知电影存在多少个打斗镜头和接吻镜头,下图中问号位置是该未知电影出现的镜头数

②之后计算未知电影与样本集中其他电影的距离(相似度),具体算法先忽略,结果如下表所示:
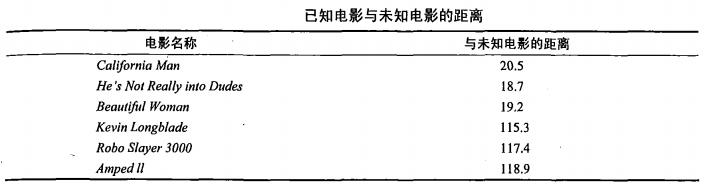
③将相似度列表排序,选出前k个最相似的样本。此处我们假设k=3,将上表中的相似度进行排序后前3分别是:He’s Not Really into Dudes,Beautiful Woman,California Man。
④统计最相似样本的分类。此处很容易知道这3个样本均为爱情片。
⑤将分类最多的类别作为未知电影的分类。那么我们就得出结论,未知电影属于爱情片。
2 代码实现
2.1 k-近邻简单分类的应用
2.1.1 算法一般流程

2.1.2 Python实现代码及注释
1 #coding=UTF8 2 from numpy import * 3 import operator 4 5 def createDataSet(): 6 """ 7 函数作用:构建一组训练数据(训练样本),共4个样本 8 同时给出了这4个样本的标签,及labels 9 """ 10 group = array([ 11 [1.0, 1.1], 12 [1.0, 1.0], 13 [0. , 0. ], 14 [0. , 0.1] 15 ]) 16 labels = ['A', 'A', 'B', 'B'] 17 return group, labels 18 19 def classify0(inX, dataset, labels, k): 20 """ 21 inX 是输入的测试样本,是一个[x, y]样式的 22 dataset 是训练样本集 23 labels 是训练样本标签 24 k 是top k最相近的 25 """ 26 # shape返回矩阵的[行数,列数], 27 # 那么shape[0]获取数据集的行数, 28 # 行数就是样本的数量 29 dataSetSize = dataset.shape[0] 30 31 """ 32 下面的求距离过程就是按照欧氏距离的公式计算的。 33 即 根号(x^2+y^2) 34 """ 35 # tile属于numpy模块下边的函数 36 # tile(A, reps)返回一个shape=reps的矩阵,矩阵的每个元素是A 37 # 比如 A=[0,1,2] 那么,tile(A, 2)= [0, 1, 2, 0, 1, 2] 38 # tile(A,(2,2)) = [[0, 1, 2, 0, 1, 2], 39 # [0, 1, 2, 0, 1, 2]] 40 # tile(A,(2,1,2)) = [[[0, 1, 2, 0, 1, 2]], 41 # [[0, 1, 2, 0, 1, 2]]] 42 # 上边那个结果的分开理解就是: 43 # 最外层是2个元素,即最外边的[]中包含2个元素,类似于[C,D],而此处的C=D,因为是复制出来的 44 # 然后C包含1个元素,即C=[E],同理D=[E] 45 # 最后E包含2个元素,即E=[F,G],此处F=G,因为是复制出来的 46 # F就是A了,基础元素 47 # 综合起来就是(2,1,2)= [C, C] = [[E], [E]] = [[[F, F]], [[F, F]]] = [[[A, A]], [[A, A]]] 48 # 这个地方就是为了把输入的测试样本扩展为和dataset的shape一样,然后就可以直接做矩阵减法了。 49 # 比如,dataset有4个样本,就是4*2的矩阵,输入测试样本肯定是一个了,就是1*2,为了计算输入样本与训练样本的距离 50 # 那么,需要对这个数据进行作差。这是一次比较,因为训练样本有n个,那么就要进行n次比较; 51 # 为了方便计算,把输入样本复制n次,然后直接与训练样本作矩阵差运算,就可以一次性比较了n个样本。 52 # 比如inX = [0,1],dataset就用函数返回的结果,那么 53 # tile(inX, (4,1))= [[ 0.0, 1.0], 54 # [ 0.0, 1.0], 55 # [ 0.0, 1.0], 56 # [ 0.0, 1.0]] 57 # 作差之后 58 # diffMat = [[-1.0,-0.1], 59 # [-1.0, 0.0], 60 # [ 0.0, 1.0], 61 # [ 0.0, 0.9]] 62 diffMat = tile(inX, (dataSetSize, 1)) - dataset 63 64 # diffMat就是输入样本与每个训练样本的差值,然后对其每个x和y的差值进行平方运算。 65 # diffMat是一个矩阵,矩阵**2表示对矩阵中的每个元素进行**2操作,即平方。 66 # sqDiffMat = [[1.0, 0.01], 67 # [1.0, 0.0 ], 68 # [0.0, 1.0 ], 69 # [0.0, 0.81]] 70 sqDiffMat = diffMat ** 2 71 72 # axis=1表示按照横轴,sum表示累加,即按照行进行累加。 73 # sqDistance = [[1.01], 74 # [1.0 ], 75 # [1.0 ], 76 # [0.81]] 77 sqDistance = sqDiffMat.sum(axis=1) 78 79 # 对平方和进行开根号 80 distance = sqDistance ** 0.5 81 82 # 按照升序进行快速排序,返回的是原数组的下标。 83 # 比如,x = [30, 10, 20, 40] 84 # 升序排序后应该是[10,20,30,40],他们的原下标是[1,2,0,3] 85 # 那么,numpy.argsort(x) = [1, 2, 0, 3] 86 sortedDistIndicies = distance.argsort() 87 88 # 存放最终的分类结果及相应的结果投票数 89 classCount = {} 90 91 # 投票过程,就是统计前k个最近的样本所属类别包含的样本个数 92 for i in range(k): 93 # index = sortedDistIndicies[i]是第i个最相近的样本下标 94 # voteIlabel = labels[index]是样本index对应的分类结果('A' or 'B') 95 voteIlabel = labels[sortedDistIndicies[i]] 96 # classCount.get(voteIlabel, 0)返回voteIlabel的值,如果不存在,则返回0 97 # 然后将票数增1 98 classCount[voteIlabel] = classCount.get(voteIlabel, 0) + 1 99 100 # 把分类结果进行排序,然后返回得票数最多的分类结果 101 sortedClassCount = sorted(classCount.items(), key=operator.itemgetter(1), reverse=True) 102 return sortedClassCount[0][0] 103 104 if __name__== "__main__": 105 # 导入数据 106 dataset, labels = createDataSet() 107 inX = [0.1, 0.1] 108 # 简单分类 109 className = classify0(inX, dataset, labels, 3) 110 print('the class of test sample is %s' %className)
2.2 在约会网站上使用k-近邻算法
2.2.1 算法一般流程

2.2.2 Python实现代码
datingTestSet.txt 文件中有1000行的约会数据,样本主要包括以下3种特征:
- 每年获得的飞行常客里程数
- 玩视频游戏所耗时间百分比
- 每周消费的冰淇淋公升数
将上述特征数据输人到分类器之前,必须将待处理数据的格式改变为分类器可以接受的格式 。在kNN.py中创建名为 file2matrix 的函数,以此来处理输人格式问题。该函数的输人为文件名字符串,输出为训练样本矩阵和类标签向量。autoNorm 为数值归一化函数,将任意取值范围的特征值转化为0到1区间内的值。最后,datingClassTest 函数是测试代码。
将下面的代码增加到 kNN.py 中。
1 def file2matrix(filename): 2 """ 3 从文件中读入训练数据,并存储为矩阵 4 """ 5 fr = open(filename) 6 arrayOlines = fr.readlines() 7 numberOfLines = len(arrayOlines) #获取 n=样本的行数 8 returnMat = zeros((numberOfLines,3)) #创建一个2维矩阵用于存放训练样本数据,一共有n行,每一行存放3个数据 9 classLabelVector = [] #创建一个1维数组用于存放训练样本标签。 10 index = 0 11 for line in arrayOlines: 12 # 把回车符号给去掉 13 line = line.strip() 14 # 把每一行数据用 分割 15 listFromLine = line.split(' ') 16 # 把分割好的数据放至数据集,其中index是该样本数据的下标,就是放到第几行 17 returnMat[index,:] = listFromLine[0:3] 18 # 把该样本对应的标签放至标签集,顺序与样本集对应。 19 classLabelVector.append(int(listFromLine[-1])) 20 index += 1 21 return returnMat,classLabelVector 22 23 def autoNorm(dataSet): 24 """ 25 训练数据归一化 26 """ 27 # 获取数据集中每一列的最小数值 28 # 以createDataSet()中的数据为例,group.min(0)=[0,0] 29 minVals = dataSet.min(0) 30 # 获取数据集中每一列的最大数值 31 # group.max(0)=[1, 1.1] 32 maxVals = dataSet.max(0) 33 # 最大值与最小的差值 34 ranges = maxVals - minVals 35 # 创建一个与dataSet同shape的全0矩阵,用于存放归一化后的数据 36 normDataSet = zeros(shape(dataSet)) 37 m = dataSet.shape[0] 38 # 把最小值扩充为与dataSet同shape,然后作差,具体tile请翻看 第三节 代码中的tile 39 normDataSet = dataSet - tile(minVals, (m,1)) 40 # 把最大最小差值扩充为dataSet同shape,然后作商,是指对应元素进行除法运算,而不是矩阵除法。 41 # 矩阵除法在numpy中要用linalg.solve(A,B) 42 normDataSet = normDataSet/tile(ranges, (m,1)) 43 return normDataSet, ranges, minVals 44 45 def datingClassTest(): 46 # 将数据集中10%的数据留作测试用,其余的90%用于训练 47 hoRatio = 0.10 48 datingDataMat,datingLabels = file2matrix('datingTestSet2.txt') #load data setfrom file 49 normMat, ranges, minVals = autoNorm(datingDataMat) 50 m = normMat.shape[0] 51 numTestVecs = int(m*hoRatio) 52 errorCount = 0.0 53 for i in range(numTestVecs): 54 classifierResult = classify0(normMat[i,:],normMat[numTestVecs:m,:],datingLabels[numTestVecs:m],3) 55 print("the classifier came back with: %d, the real answer is: %d, result is :%s" % (classifierResult, datingLabels[i],classifierResult==datingLabels[i])) 56 if (classifierResult != datingLabels[i]): errorCount += 1.0 57 print("the total error rate is: %f" % (errorCount/float(numTestVecs))) 58 print(errorCount)
2.3 手写识别系统实例
2.3.1 实例数据
为了简单起见,这里构造的系统只能识别数字0到9。需要识别的数字已经使用图形处理软件,处理成具有相同的色彩和大小 : 宽髙是32像素x 32像素的黑白图像。尽管采用文本格式存储图像不能有效地利用内存空间,但是为了方便理解,我们还是将图像转换为文本格式。
trainingDigits是2000个训练样本,testDigits是900个测试样本。
2.3.2 算法的流程


2.3.3 Python实现代码
将下面的代码增加到 kNN.py 中,img2vector 为图片转换成向量的方法,handwritingClassTest 为测试方法:
1 from os import listdir 2 def img2vector(filename): 3 """ 4 将图片数据转换为01矩阵。 5 每张图片是32*32像素,也就是一共1024个字节。 6 因此转换的时候,每行表示一个样本,每个样本含1024个字节。 7 """ 8 # 每个样本数据是1024=32*32个字节 9 returnVect = zeros((1,1024)) 10 fr = open(filename) 11 # 循环读取32行,32列。 12 for i in range(32): 13 lineStr = fr.readline() 14 for j in range(32): 15 returnVect[0,32*i+j] = int(lineStr[j]) 16 return returnVect 17 18 def handwritingClassTest(): 19 hwLabels = [] 20 # 加载训练数据 21 trainingFileList = listdir('trainingDigits') 22 m = len(trainingFileList) 23 trainingMat = zeros((m,1024)) 24 for i in range(m): 25 # 从文件名中解析出当前图像的标签,也就是数字是几 26 # 文件名格式为 0_3.txt 表示图片数字是 0 27 fileNameStr = trainingFileList[i] 28 fileStr = fileNameStr.split('.')[0] #take off .txt 29 classNumStr = int(fileStr.split('_')[0]) 30 hwLabels.append(classNumStr) 31 trainingMat[i,:] = img2vector('trainingDigits/%s' % fileNameStr) 32 # 加载测试数据 33 testFileList = listdir('testDigits') #iterate through the test set 34 errorCount = 0.0 35 mTest = len(testFileList) 36 for i in range(mTest): 37 fileNameStr = testFileList[i] 38 fileStr = fileNameStr.split('.')[0] #take off .txt 39 classNumStr = int(fileStr.split('_')[0]) 40 vectorUnderTest = img2vector('testDigits/%s' % fileNameStr) 41 classifierResult = classify0(vectorUnderTest, trainingMat, hwLabels, 3) 42 print("the classifier came back with: %d, the real answer is: %d, The predict result is: %s" % (classifierResult, classNumStr, classifierResult==classNumStr)) 43 if (classifierResult != classNumStr): errorCount += 1.0 44 print(" the total number of errors is: %d / %d" %(errorCount, mTest)) 45 print(" the total error rate is: %f" % (errorCount/float(mTest)))
k-近邻算法识别手写数字数据集,错误率为1. 2%。改变变量k的值、修改函数 handwritingClassTest 随机选取训练样本、改变训练样本的数目,都会对k-近邻算法的错误率产生影响,感兴趣的话可以改变这些变量值,观察错误率的变化。
k-近邻算法是分类数据最简单最有效的算法。它必须保存全部数据集,如果训练数据集很大,必须使用大量的存储空间。此外,由于必须对数据集中的每个数据计算距离值,实际使用时可能非常耗时。其另一个缺陷是它无法给出任何数据的基础结构信息,因此我们也无法知晓平均实例样本和典型实例样本具有什么特征。
3 应用 scikit-learn 库实现k近邻算法
1 """ 2 scikit-learn 库对knn的支持 3 数据集是iris虹膜数据集 4 """ 5 6 from sklearn.datasets import load_iris 7 from sklearn import neighbors 8 import sklearn 9 10 #查看iris数据集 11 iris = load_iris() 12 print(iris) 13 14 ''' 15 KNeighborsClassifier(n_neighbors=5, weights='uniform', 16 algorithm='auto', leaf_size=30, 17 p=2, metric='minkowski', 18 metric_params=None, n_jobs=1, **kwargs) 19 n_neighbors: 默认值为5,表示查询k个最近邻的数目 20 algorithm: {‘auto’, ‘ball_tree’, ‘kd_tree’, ‘brute’},指定用于计算最近邻的算法,auto表示试图采用最适合的算法计算最近邻 21 leaf_size: 传递给‘ball_tree’或‘kd_tree’的叶子大小 22 metric: 用于树的距离度量。默认'minkowski与P = 2(即欧氏度量) 23 n_jobs: 并行工作的数量,如果设为-1,则作业的数量被设置为CPU内核的数量 24 查看官方api:http://scikit-learn.org/dev/modules/generated/sklearn.neighbors.KNeighborsClassifier.html#sklearn.neighbors.KNeighborsClassifier 25 ''' 26 knn = neighbors.KNeighborsClassifier() 27 #训练数据集 28 knn.fit(iris.data, iris.target) 29 #训练准确率 30 score = knn.score(iris.data, iris.target) 31 32 #预测 33 predict = knn.predict([[0.1,0.2,0.3,0.4]]) 34 #预测,返回概率数组 35 predict2 = knn.predict_proba([[0.1,0.2,0.3,0.4]]) 36 37 print(predict) 38 print(iris.target_names[predict])
代码解释参考原贴:http://blog.csdn.net/niuwei22007/article/details/49703719