数字三角形

其实数字三角形网上的代码无数，别人也讲得很好，而且这个题的难度不大，但是这道题作为入门动态规划和学习使用备忘录以及递归到递推的转换真的很适合，而且我感觉毕竟自己写的东西除了记忆更深刻以外，下次回顾的时候也就更加亲切，过往的记忆很快被打通，所以我决定还是把自己写的代码再上传上去，起到总结和复习的作用。

1按照思路可以写出使用递归的代码如下

#include<bits/stdc++.h>
using namespace std;
int array[100][100];
int n;
int path[100]={0};
int f(int r,int j){
  if(r==n-1){
    return array[r][j];
  }
  int num1=f(r+1,j);
  int num2=f(r+1,j+1);
  if(num1>num2){
    return num1+array[r][j];
  }
  else{
    return num2+array[r][j];
  }
}
int main()
{

    cin >> n;
    memset(array,0,sizeof(array));
    for(int i=0;i<n;i++){
        for(int j=0;j<=i;j++){
          cin >> array[i][j];
        }
    }
    cout << f(0,0);
    return 0;
}

此时代码的复杂度为2^n显然需要改进

分析如下

2根据思路可知利用备忘录算法可以大大降低复杂度，代码如下

#include<bits/stdc++.h>
using namespace std;
int array[100][100];
int n;
int path[100][100];//用来表示该位置有没有计算过，没有就计算，有就直接使用
int f(int r,int j){
  if(r==n-1){
    return array[r][j];
  }
  if(path[r+1][j]==-1){//没有就计算
    path[r+1][j]=f(r+1,j);
  }
  if(path[r+1][j+1]==-1){
    path[r+1][j+1]=f(r+1,j+1);
  }
  if(path[r+1][j]>path[r+1][j+1]){//直接使用计算过的
    return path[r+1][j]+array[r][j];
  }
  else{
    return path[r+1][j+1]+array[r][j];
  }
}
int main()
{
    cin >> n;
    memset(array,0,sizeof(array));
    for(int i=0;i<100;i++){
        for(int j=0;j<100;j++){
            path[i][j]=-1;
        }
    }
    for(int i=0;i<n;i++){
        for(int j=0;j<=i;j++){
          cin >> array[i][j];
        }
    }
    cout << f(0,0);
    return 0;
}

3递推法

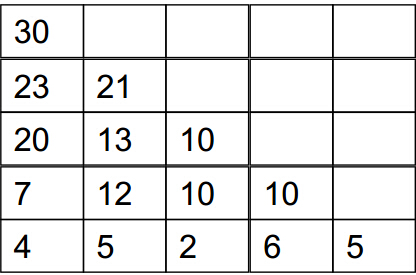
从底向上递推，出最后一行外，每一行的每个点的最大值等于自身加上下面一行对应左右两个点的最大值，从下往上递推，最顶部的即所求。比如下图所示。首先最后一行的最大值就是它本身。倒数第二行第一个数7就是输入的倒二行的第一个数2 + 4 和 2 +5 取最大值 。逐步递推到顶部。

#include<bits/stdc++.h>
using namespace std;
int array[100][100];
int main()
{
    int n;
    cin >> n;
    memset(array,0,sizeof(array));
    for(int i=0;i<n;i++){
        for(int j=0;j<=i;j++){
            cin >>array[i][j];
        }
    }
    for(int i=n-2;i>=0;i--){
        for(int j=0;j<=n-2;j++){//对左右两边的数字进行选择，较大的加上去
            if(array[i+1][j]>array[i+1][j+1])
                array[i][j]+=array[i+1][j];
             else{
                array[i][j]+=array[i+1][j+1];
             }
        }
    }
    cout << array[0][0] << endl;
    return 0;
}

 4使用递推法并打印路径

因为上一行都是加上下一行的较大者才保证上一行值最大，所以我们可以通过从第一行向下比较较大者便是经过的路径

即

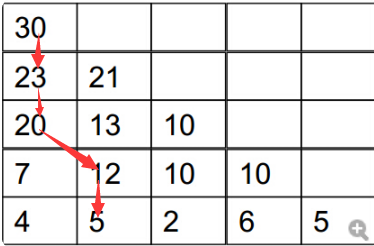
等价于

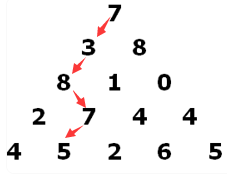
代码如下

#include<bits/stdc++.h>
using namespace std;
int array[100][100];
int array1[100][100];
int main()
{
    int n;
    cin >> n;
    memset(array,0,sizeof(array));
    memset(array1,0,sizeof(array1));
    for(int i=0;i<n;i++){
        for(int j=0;j<=i;j++){
            cin >>array[i][j];
            array1[i][j]=array[i][j];
        }
    }
    for(int i=n-2;i>=0;i--){
        for(int j=0;j<=n-2;j++){//对左右两边的数字进行选择，较大的加上去
            if(array[i+1][j]>array[i+1][j+1])
                array[i][j]+=array[i+1][j];
             else{
                array[i][j]+=array[i+1][j+1];
             }
        }
    }
     cout << array[0][0] << endl;
     cout << "路径为："<< endl;
    cout << array1[0][0]<< "--->";
    int u1=0;
    int u2=0;

    for(int i=u1;i<n-1;i++){
        for(int j=u2;j<=i;j++){
            if(array[i+1][j]>array[i+1][j+1]){
                cout << array1[i+1][j] << "--->";
                u2=j;
                break;
            }
            else{
                cout << array1[i+1][j+1] << "--->";
                u2=j+1;
              break;
            }
        }
    }
    cout << "结束";
    return 0;
}

运行结果截图

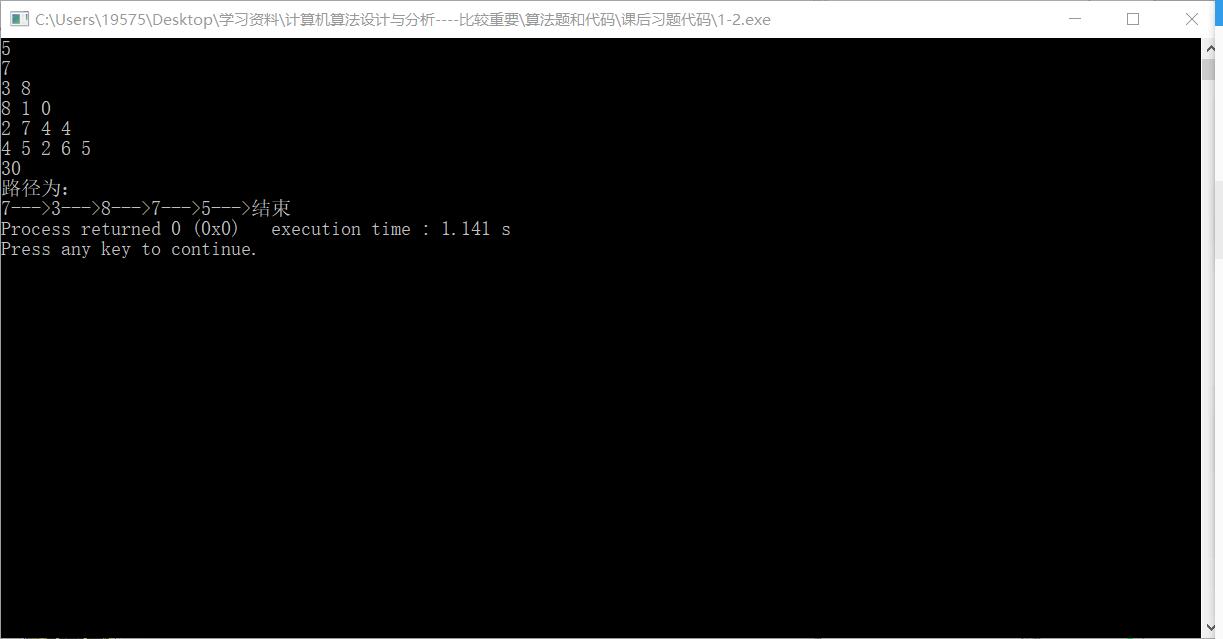
 递推时间复杂度要优于递归