1. sigmod函数
函数公式和图表如下图
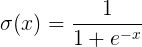

在sigmod函数中我们可以看到,其输出是在(0,1)这个开区间内,这点很有意思,可以联想到概率,但是严格意义上讲,不要当成概率。sigmod函数曾经是比较流行的,它可以想象成一个神经元的放电率,在中间斜率比较大的地方是神经元的敏感区,在两边斜率很平缓的地方是神经元的抑制区。
当然,流行也是曾经流行,这说明函数本身是有一定的缺陷的。
1) 当输入稍微远离了坐标原点,函数的梯度就变得很小了,几乎为零。在神经网络反向传播的过程中,我们都是通过微分的链式法则来计算各个权重w的微分的。当反向传播经过了sigmod函数,这个链条上的微分就很小很小了,况且还可能经过很多个sigmod函数,最后会导致权重w对损失函数几乎没影响,这样不利于权重的优化,这个问题叫做梯度饱和,也可以叫梯度弥散。
2) 函数输出不是以0为中心的,这样会使权重更新效率降低。对于这个缺陷,在斯坦福的课程里面有详细的解释。
3) sigmod函数要进行指数运算,这个对于计算机来说是比较慢的。
2.tanh函数
tanh函数公式和曲线如下
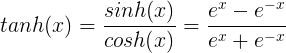
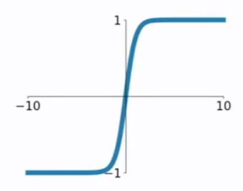
tanh是双曲正切函数,tanh函数和sigmod函数的曲线是比较相近的,咱们来比较一下看看。首先相同的是,这两个函数在输入很大或是很小的时候,输出都几乎平滑,梯度很小,不利于权重更新;不同的是输出区间,tanh的输出区间是在(-1,1)之间,而且整个函数是以0为中心的,这个特点比sigmod的好。
一般二分类问题中,隐藏层用tanh函数,输出层用sigmod函数。不过这些也都不是一成不变的,具体使用什么激活函数,还是要根据具体的问题来具体分析,还是要靠调试的。
3.ReLU函数
ReLU函数公式和曲线如下
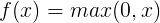
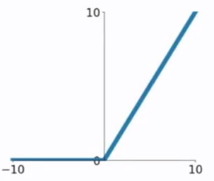
ReLU(Rectified Linear Unit)函数是目前比较火的一个激活函数,相比于sigmod函数和tanh函数,它有以下几个优点:
1) 在输入为正数的时候,不存在梯度饱和问题。
2) 计算速度要快很多。ReLU函数只有线性关系,不管是前向传播还是反向传播,都比sigmod和tanh要快很多。(sigmod和tanh要计算指数,计算速度会比较慢)
当然,缺点也是有的:
1) 当输入是负数的时候,ReLU是完全不被激活的,这就表明一旦输入到了负数,ReLU就会死掉。这样在前向传播过程中,还不算什么问题,有的区域是敏感的,有的是不敏感的。但是到了反向传播过程中,输入负数,梯度就会完全到0,这个和sigmod函数、tanh函数有一样的问题。
2) 我们发现ReLU函数的输出要么是0,要么是正数,这也就是说,ReLU函数也不是以0为中心的函数。
4.ELU函数
ELU函数公式和曲线如下图
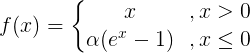
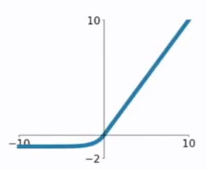
ELU函数是针对ReLU函数的一个改进型,相比于ReLU函数,在输入为负数的情况下,是有一定的输出的,而且这部分输出还具有一定的抗干扰能力。这样可以消除ReLU死掉的问题,不过还是有梯度饱和和指数运算的问题。
5.PReLU函数
PReLU函数公式和曲线如下图
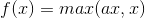

PReLU也是针对ReLU的一个改进型,在负数区域内,PReLU有一个很小的斜率,这样也可以避免ReLU死掉的问题。相比于ELU,PReLU在负数区域内是线性运算,斜率虽然小,但是不会趋于0,这算是一定的优势吧。
我们看PReLU的公式,里面的参数α一般是取0~1之间的数,而且一般还是比较小的,如零点零几。当α=0.01时,我们叫PReLU为Leaky ReLU,算是PReLU的一种特殊情况吧。
总体来看,这些激活函数都有自己的优点和缺点,没有一条说法表明哪些就是不行,哪些激活函数就是好的,所有的好坏都要自己去实验中得到。
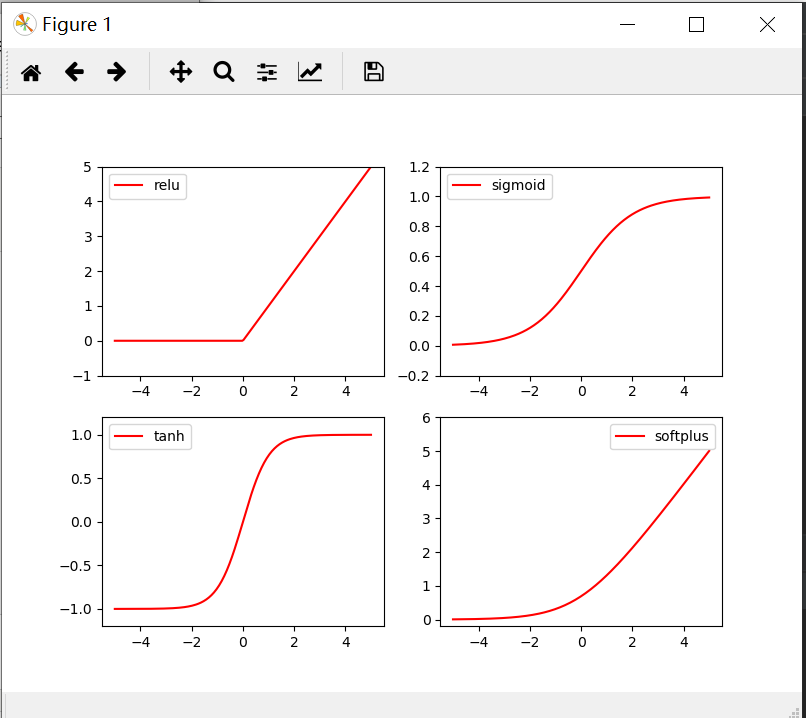
画出激励函数的代码如下
import torch from torch.autograd import Variable import matplotlib.pyplot as plt import torch.nn.functional as F x= torch.linspace(-5,5,200) x= Variable(x) x_np=x.data.numpy() y_relu = torch.relu(x).data.numpy() y_sigmoid =torch.sigmoid(x).data.numpy() y_tanh = torch.tanh(x).data.numpy() y_softplus = F.softplus(x).data.numpy() plt.figure(1,figsize=(8,6)) plt.subplot(221) plt.plot(x_np,y_relu,c='red',label='relu') plt.ylim(-1,5) plt.legend(loc='best') plt.subplot(222) plt.plot(x_np,y_sigmoid,c='red',label='sigmoid') plt.ylim(-0.2,1.2) plt.legend(loc='best') plt.subplot(223) plt.plot(x_np,y_tanh,c='red',label='tanh') plt.ylim(-1.2,1.2) plt.legend(loc='best') plt.subplot(224) plt.plot(x_np,y_softplus,c='red',label='softplus') plt.ylim(-0.2,6) plt.legend(loc='best') plt.show()