漫画算法_小灰灰面试

倒排索引

   在搜索引擎中每个文件都对应一个文件ID，文件内容被表示为一系列关键词的集合（实际上在搜索引擎索引库中，关键词也已经转换为关键词ID）。例如“文档1”经过分词，提取了20个关键词，每个关键词都会记录它在文档中的出现次数和出现位置。

     得到正向索引的结构如下：

       “文档1”的ID > 单词1：出现次数，出现位置列表；单词2：出现次数，出现位置列表；…………。

       “文档2”的ID > 此文档出现的关键词列表。

 

　　一般是通过key，去找value。

      当用户在主页上搜索关键词“华为手机”时，假设只存在正向索引（forward index），那么就需要扫描索引库中的所有文档，找出所有包含关键词“华为手机”的文档，再根据打分模型进行打分，排出名次后呈现给用户。因为互联网上收录在搜索引擎中的文档的数目是个天文数字，这样的索引结构根本无法满足实时返回排名结果的要求。

       所以，搜索引擎会将正向索引重新构建为倒排索引，即把文件ID对应到关键词的映射转换为关键词到文件ID的映射，每个关键词都对应着一系列的文件，这些文件中都出现这个关键词。

       得到倒排索引的结构如下：

       “关键词1”：“文档1”的ID，“文档2”的ID，…………。

       “关键词2”：带有此关键词的文档ID列表。

 

　　从词的关键字，去找文档。

1.单词——文档矩阵

      单词-文档矩阵是表达两者之间所具有的一种包含关系的概念模型，图1展示了其含义。图3-1的每列代表一个文档，每行代表一个单词，打对勾的位置代表包含关系。

　　　　　　　　　　　　

　　　　　　　　  　　　　　　　　　　　　　　　　图1 单词-文档矩阵

     从纵向即文档这个维度来看，每列代表文档包含了哪些单词，比如文档1包含了词汇1和词汇4，而不包含其它单词。从横向即单词这个维度来看，每行代表了哪些文档包含了某个单词。比如对于词汇1来说，文档1和文档4中出现过单词1，而其它文档不包含词汇1。矩阵中其它的行列也可作此种解读。

    搜索引擎的索引其实就是实现“单词-文档矩阵”的具体数据结构。可以有不同的方式来实现上述概念模型，比如“倒排索引”、“签名文件”、“后缀树”等方式。但是各项实验数据表明，“倒排索引”是实现单词到文档映射关系的最佳实现方式，所以本博文主要介绍“倒排索引”的技术细节。

2.倒排索引基本概念

       文档(Document)：一般搜索引擎的处理对象是互联网网页，而文档这个概念要更宽泛些，代表以文本形式存在的存储对象，相比网页来说，涵盖更多种形式，比如Word，PDF，html，XML等不同格式的文件都可以称之为文档。再比如一封邮件，一条短信，一条微博也可以称之为文档。在本书后续内容，很多情况下会使用文档来表征文本信息。

       文档集合(Document Collection)：由若干文档构成的集合称之为文档集合。比如海量的互联网网页或者说大量的电子邮件都是文档集合的具体例子。

       文档编号(Document ID)：在搜索引擎内部，会将文档集合内每个文档赋予一个唯一的内部编号，以此编号来作为这个文档的唯一标识，这样方便内部处理，每个文档的内部编号即称之为“文档编号”，后文有时会用DocID来便捷地代表文档编号。

       单词编号(Word ID)：与文档编号类似，搜索引擎内部以唯一的编号来表征某个单词，单词编号可以作为某个单词的唯一表征。

       倒排索引(Inverted Index)：倒排索引是实现“单词-文档矩阵”的一种具体存储形式，通过倒排索引，可以根据单词快速获取包含这个单词的文档列表。倒排索引主要由两个部分组成：“单词词典”和“倒排文件”。

       单词词典(Lexicon)：搜索引擎的通常索引单位是单词，单词词典是由文档集合中出现过的所有单词构成的字符串集合，单词词典内每条索引项记载单词本身的一些信息以及指向“倒排列表”的指针。

       倒排列表(PostingList)：倒排列表记载了出现过某个单词的所有文档的文档列表及单词在该文档中出现的位置信息，每条记录称为一个倒排项(Posting)。根据倒排列表，即可获知哪些文档包含某个单词。

       倒排文件(Inverted File)：所有单词的倒排列表往往顺序地存储在磁盘的某个文件里，这个文件即被称之为倒排文件，倒排文件是存储倒排索引的物理文件。

     关于这些概念之间的关系，通过图2可以比较清晰的看出来。

　　　　　　　　　　　　　　

3.倒排索引简单实例

      倒排索引从逻辑结构和基本思路上来讲非常简单。下面我们通过具体实例来进行说明，使得读者能够对倒排索引有一个宏观而直接的感受。

      假设文档集合包含五个文档，每个文档内容如图3所示，在图中最左端一栏是每个文档对应的文档编号。我们的任务就是对这个文档集合建立倒排索引。

　　　　　　　　　　　　　　

 　　　　　　　　　　　　　　　　　　　　　　　　　　图3   文档集合

　　中文和英文等语言不同，单词之间没有明确分隔符号，所以首先要用分词系统将文档自动切分成单词序列。这样每个文档就转换为由单词序列构成的数据流，为了系统后续处理方便，需要对每个不同的单词赋予唯一的单词编号，同时记录下哪些文档包含这个单词，在如此处理结束后，我们可以得到最简单的倒排索引（参考图3-4）。在图4中，“单词ID”一栏记录了每个单词的单词编号，第二栏是对应的单词，第三栏即每个单词对应的倒排列表。比如单词“谷歌”，其单词编号为1，倒排列表为{1,2,3,4,5}，说明文档集合中每个文档都包含了这个单词。

　　　　　　　　　　　　　　

　　　　　　　　　　　　　　　　　　　　　　　　　　　　图4   简单的倒排索引

　　之所以说图4所示倒排索引是最简单的，是因为这个索引系统只记载了哪些文档包含某个单词，而事实上，索引系统还可以记录除此之外的更多信息。图5是一个相对复杂些的倒排索引，与图4的基本索引系统比，在单词对应的倒排列表中不仅记录了文档编号，还记载了单词频率信息（TF），即这个单词在某个文档中的出现次数，之所以要记录这个信息，是因为词频信息在搜索结果排序时，计算查询和文档相似度是很重要的一个计算因子，所以将其记录在倒排列表中，以方便后续排序时进行分值计算。在图5的例子里，单词“创始人”的单词编号为7，对应的倒排列表内容为：（3:1），其中的3代表文档编号为3的文档包含这个单词，数字1代表词频信息，即这个单词在3号文档中只出现过1次，其它单词对应的倒排列表所代表含义与此相同。

　　　　　　　　　　　　　　

　　　　　　　　　　　　　　　　　　　　　　　　　　　　图 5 带有单词频率信息的倒排索引

 　　实用的倒排索引还可以记载更多的信息，图6所示索引系统除了记录文档编号和单词频率信息外，额外记载了两类信息，即每个单词对应的“文档频率信息”（对应图6的第三栏）以及在倒排列表中记录单词在某个文档出现的位置信息。

　　　　　　　　　　　　　　　　　　

 　　　　　　　　　　　　　　　　　　　　　　图6   带有单词频率、文档频率和出现位置信息的倒排索引

   “文档频率信息”代表了在文档集合中有多少个文档包含某个单词，之所以要记录这个信息，其原因与单词频率信息一样，这个信息在搜索结果排序计算中是非常重要的一个因子。而单词在某个文档中出现的位置信息并非索引系统一定要记录的，在实际的索引系统里可以包含，也可以选择不包含这个信息，之所以如此，因为这个信息对于搜索系统来说并非必需的，位置信息只有在支持“短语查询”的时候才能够派上用场。

     以单词“拉斯”为例，其单词编号为8，文档频率为2，代表整个文档集合中有两个文档包含这个单词，对应的倒排列表为：{(3;1;<4>)，(5;1;<4>)},其含义为在文档3和文档5出现过这个单词，单词频率都为1，单词“拉斯”在两个文档中的出现位置都是4，即文档中第四个单词是“拉斯”。

     图6所示倒排索引已经是一个非常完备的索引系统，实际搜索系统的索引结构基本如此，区别无非是采取哪些具体的数据结构来实现上述逻辑结构。

     有了这个索引系统，搜索引擎可以很方便地响应用户的查询，比如用户输入查询词“Facebook”，搜索系统查找倒排索引，从中可以读出包含这个单词的文档，这些文档就是提供给用户的搜索结果，而利用单词频率信息、文档频率信息即可以对这些候选搜索结果进行排序，计算文档和查询的相似性，按照相似性得分由高到低排序输出，此即为搜索系统的部分内部流程，具体实现方案本书第五章会做详细描述。

1.  BitMap

Bit-map的基本思想就是用一个bit位来标记某个元素对应的Value，而Key即是该元素。由于采用了Bit为单位来存储数据，因此在存储空间方面，可以大大节省。（PS：划重点 节省存储空间）

假设有这样一个需求：在20亿个随机整数中找出某个数m是否存在其中，并假设32位操作系统，4G内存

在Java中，int占4字节，1字节=8位（1 byte = 8 bit）

如果每个数字用int存储，那就是20亿个int，因而占用的空间约为  (2000000000*4/1024/1024/1024)≈7.45G

如果按位存储就不一样了，20亿个数就是20亿位，占用空间约为  (2000000000/8/1024/1024/1024)≈0.233G

高下立判，无需多言

那么，问题来了，如何表示一个数呢？

刚才说了，每一位表示一个数，0表示不存在，1表示存在，这正符合二进制

这样我们可以很容易表示{1,2,4,6}这几个数：

计算机内存分配的最小单位是字节，也就是8位，那如果要表示{12,13,15}怎么办呢？

当然是在另一个8位上表示了：

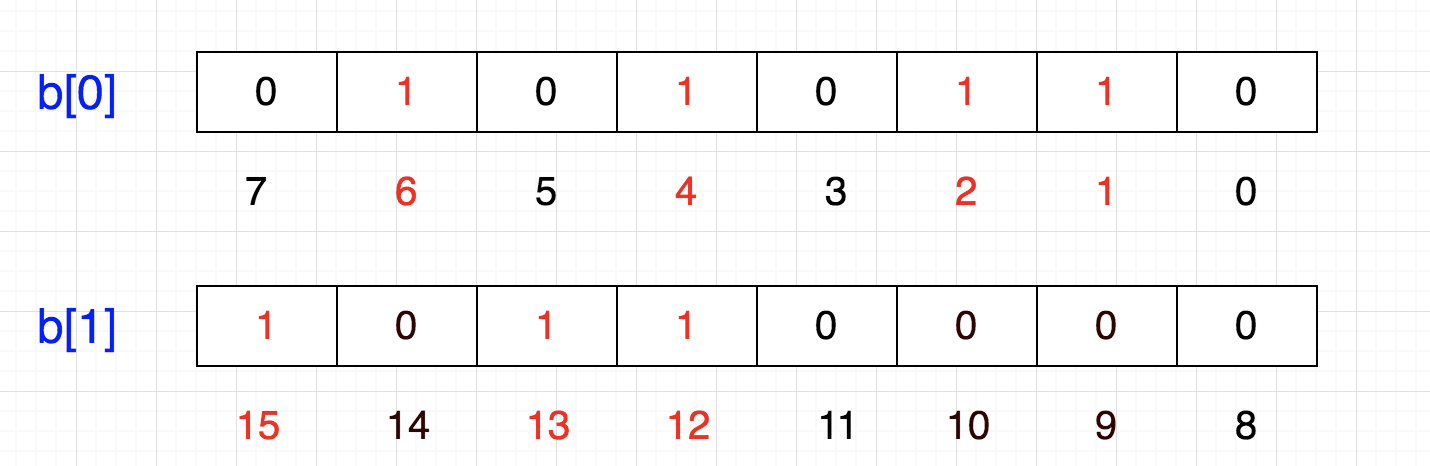
这样的话，好像变成一个二维数组了

1个int占32位，那么我们只需要申请一个int数组长度为 int tmp[1+N/32] 即可存储，其中N表示要存储的这些数中的最大值，于是乎：

tmp[0]：可以表示0~31

tmp[1]：可以表示32~63

tmp[2]：可以表示64~95

。。。

如此一来，给定任意整数M，那么M/32就得到下标，M%32就知道它在此下标的哪个位置

添加 

这里有个问题，我们怎么把一个数放进去呢？例如，想把5这个数字放进去，怎么做呢？

首先，5/32=0，5%32=5，也是说它应该在tmp[0]的第5个位置，那我们把1向左移动5位，然后按位或

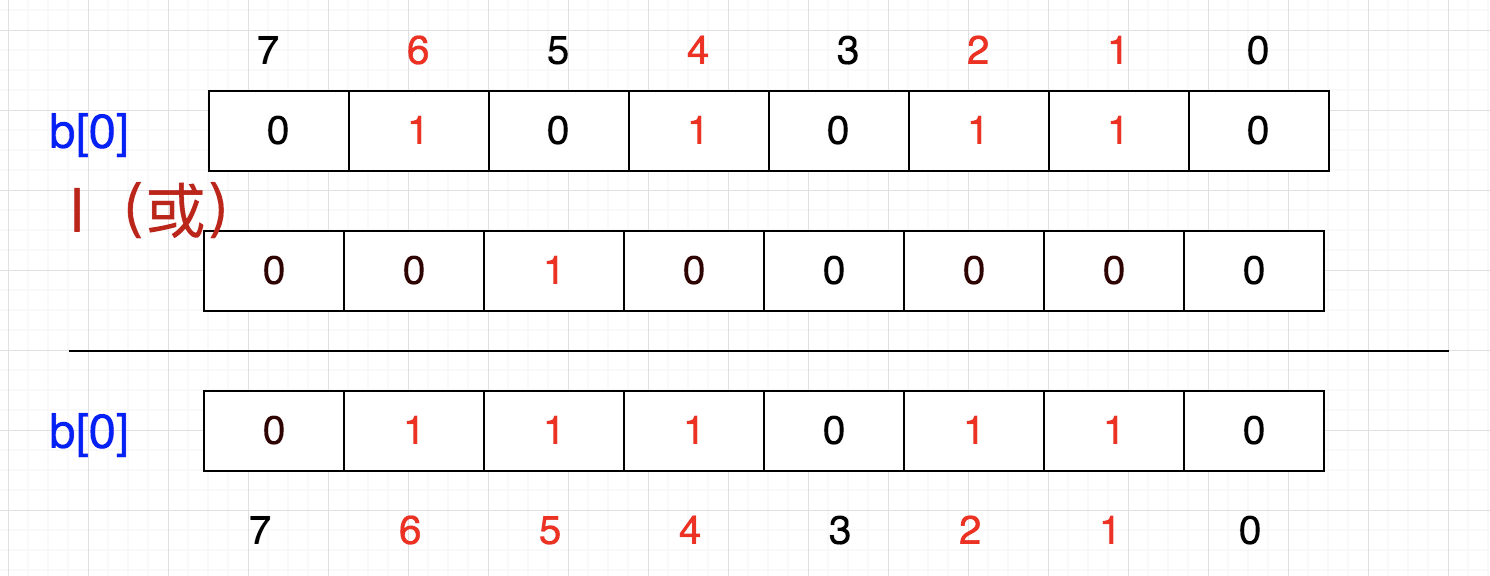
换成二进制就是

这就相当于 86 | 32 = 118

86 | (1<<5) = 118

b[0] = b[0] | (1<<5)

也就是说，要想插入一个数，将1左移带代表该数字的那一位，然后与原数进行按位或操作

化简一下，就是 86 + (5/8) | (1<<(5%8))

因此，公式可以概括为：p + (i/8)|(1<<(i%8)) 其中，p表示现在的值，i表示待插入的数

清除 

以上是添加，那如果要清除该怎么做呢？

还是上面的例子，假设我们要6移除，该怎么做呢？

从图上看，只需将该数所在的位置为0即可

1左移6位，就到达6这个数字所代表的位，然后按位取反，最后与原数按位与，这样就把该位置为0了

b[0] = b[0] & (~(1<<6))

b[0] = b[0] & (~(1<<(i%8)))

查找 

前面我们也说了，每一位代表一个数字，1表示有（或者说存在），0表示无（或者说不存在）。通过把该为置为1或者0来达到添加和清除的小伙，那么判断一个数存不存在就是判断该数所在的位是0还是1

假设，我们想知道3在不在，那么只需判断 b[0] & (1<<3) 如果这个值是0，则不存在，如果是1，就表示存在

2.  Bitmap有什么用

大量数据的快速排序、查找、去重

快速排序

假设我们要对0-7内的5个元素(4,7,2,5,3)排序（这里假设这些元素没有重复）,我们就可以采用Bit-map的方法来达到排序的目的。

要表示8个数，我们就只需要8个Bit（1Bytes），首先我们开辟1Byte的空间，将这些空间的所有Bit位都置为0，然后将对应位置为1。

最后，遍历一遍Bit区域，将该位是一的位的编号输出（2，3，4，5，7），这样就达到了排序的目的，时间复杂度O(n)。

优点：

• 运算效率高，不需要进行比较和移位；
• 占用内存少，比如N=10000000；只需占用内存为N/8=1250000Byte=1.25M

缺点：

• 所有的数据不能重复。即不可对重复的数据进行排序和查找。
• 只有当数据比较密集时才有优势

快速去重

20亿个整数中找出不重复的整数的个数，内存不足以容纳这20亿个整数。 

首先，根据“内存空间不足以容纳这05亿个整数”我们可以快速的联想到Bit-map。下边关键的问题就是怎么设计我们的Bit-map来表示这20亿个数字的状态了。其实这个问题很简单，一个数字的状态只有三种，分别为不存在，只有一个，有重复。因此，我们只需要2bits就可以对一个数字的状态进行存储了，假设我们设定一个数字不存在为00，存在一次01，存在两次及其以上为11。那我们大概需要存储空间2G左右。

接下来的任务就是把这20亿个数字放进去（存储），如果对应的状态位为00，则将其变为01，表示存在一次；如果对应的状态位为01，则将其变为11，表示已经有一个了，即出现多次；如果为11，则对应的状态位保持不变，仍表示出现多次。

最后，统计状态位为01的个数，就得到了不重复的数字个数，时间复杂度为O(n)。

快速查找

这就是我们前面所说的了，int数组中的一个元素是4字节占32位，那么除以32就知道元素的下标，对32求余数（%32）就知道它在哪一位，如果该位是1，则表示存在。

小结&回顾

Bitmap主要用于快速检索关键字状态，通常要求关键字是一个连续的序列（或者关键字是一个连续序列中的大部分）， 最基本的情况，使用1bit表示一个关键字的状态（可标示两种状态），但根据需要也可以使用2bit（表示4种状态），3bit（表示8种状态）。

Bitmap的主要应用场合：表示连续（或接近连续，即大部分会出现）的关键字序列的状态（状态数/关键字个数  越小越好）。

32位机器上，对于一个整型数，比如int a=1 在内存中占32bit位，这是为了方便计算机的运算。但是对于某些应用场景而言，这属于一种巨大的浪费，因为我们可以用对应的32bit位对应存储十进制的0-31个数，而这就是Bit-map的基本思想。Bit-map算法利用这种思想处理大量数据的排序、查询以及去重。

 判断链表是否有环

(2条消息) 判断链表是否有环（简单）_小布丁value的博客-CSDN博客

package 小灰灰;

import java.util.HashSet;
import java.util.Set;

/**
 * 判断单链表是否有环和环的大小
 */
public class hasCycle {

    public boolean solution1(ListNode begin) {    //保证时间效率最高，但是会开辟额外的空间，通过声明一个set,把遍历的数据放入set
        Set<Integer> set = new HashSet();//里面，，每遍历一次数据就判断是否存在，不存在则加入，存在则存在环
        boolean cycle = false;  //是否含有环

        while (true) {
            if (set.contains(begin.data)) {
                cycle = true;
                break;
            } else {
                if (begin.next == null) {
                    break;
                } else {
                    set.add(begin.data);
                    begin = begin.next;
                }
            }
        }
        return cycle;

    }

    /**
     *
     * @param begin，起始节点
     * @return 布尔值，是否有环
     * 是否含有环,思想为追及问题，两个人速度不同，那么必然有相遇的时刻。
     */
    public boolean solution2(ListNode begin) {
        ListNode index1 = begin;    //速度为1的指针
        ListNode index2 = begin;    //速度为2的指针
        Set<Integer> set = new HashSet();
        boolean cycle = false;  //是否含有环

        while (true) {
            if(index1.next != null){
                index1 = index1.next;
            }else{
                break;
            }
            if(index2.next != null){
                index2= index2.next;
                if(index2.next!=null){
                    index2 = index2.next;
                }else{
                    break;
                }
            }else{
                break;
            }
         if(index1.data== index2.data){
             cycle = true;
             break;
         }
        }

        return cycle;

    }
    /**
     * @param  起始节点
     * @return int值，环的大小，没有环返回0
     *  是否含有环,思想为追及问题，两个人速度不同，那么必然有相遇的时刻。一个速度为两一个速度的两倍，则快得必然比慢的先走
     *     一圈
     */
    public int solution3(ListNode begin) {
        ListNode index1 = begin;    //速度为1的指针
        ListNode index2 = begin;    //速度为2的指针
        Set<Integer> set = new HashSet();
        int cycleStep = 0;      //计算环的大小
        int meet = 0;       //计算相遇的次数
        while (true) {
            if(index1.next != null){
                index1 = index1.next;
                if(meet==1){
                    cycleStep++;
                }
            }else{
                break;
            }
            if(index2.next != null){
                index2= index2.next;
                if(index2.next!=null){
                    index2 = index2.next;
                }else{
                    break;
                }
            }else{
                break;
            }
            if(index1.data== index2.data){
               meet++;
               if(meet>=2)
                break;
            }
        }

        return cycleStep;
    }

    /**
     * 入环点，2（D+s1）=D+s1+n(s1+s2)。推理得到D=(n-1)(s1+s2)+s2,其中D是从出发点到入环点的距离，s1是首次相遇点，s2是首次相遇点到入环点的距离
     * 代码略
     */

    public static void main(String[] args) {
        hasCycle hasCycle = new hasCycle();

        ListNode node7 = new ListNode(1);
        ListNode node6 = new ListNode(2);
        ListNode node5 = new ListNode(3);
        ListNode node4 = new ListNode(4);
        ListNode node3 = new ListNode(5);
        ListNode node2 = new ListNode(6);
        ListNode node1 = new ListNode(7);
//        node7.next = null;
        node7.next = node4;
        node6.next = node7;
        node5.next = node6;
        node4.next = node5;
        node3.next = node4;
        node2.next = node3;
        node1.next = node2;

        System.out.println(hasCycle.solution1(node1));
        System.out.println(hasCycle.solution2(node1));
        System.out.println(hasCycle.solution3(node1));
    }
}

class ListNode {
    int data;
    ListNode next;

    public ListNode(int data) {
        this.data = data;
        this.next = next;
    }
}

最小栈的实现

package 小灰灰;

import java.util.Scanner;
import java.util.Stack;

/**
 * 实现一个栈，具有出栈，入栈，取栈中最小值的功能.
 * 实现思想：一个栈用来维护数据，另一个栈用来维护最小值的下标，每当加入或者出栈则同时对两个栈进行更新。
 */
public class StackMinValue {

    public static void init(Stack stack1,Stack stack2){     //初始化，栈最小值
        int n;  //进栈几个数
        int value;    //用户每次进栈的数字
        Scanner scanner = new Scanner(System.in);
        n = scanner.nextInt();
        while (n--!=0){
            value = scanner.nextInt();
            StackMinValue.push(stack1,stack2,value);
        }
    }

    public static int get_min(Stack stack1, Stack stack2){

        int num = (int) stack1.get((int)stack2.lastElement());
        return num;
    }

    public static void pop(Stack stack,Stack stack2){//出栈，最小值被弹出，则对两个栈同时更新
        if(stack.size()!=0){
            stack.pop();
            int size = stack.size();
            int element = (int) stack2.lastElement();
            if(size <= element){
                stack2.pop();
            }
        }

    }

    public static void push(Stack stack,Stack stack2,int value){
        if(stack.size()==0){
            stack.push(value);
            stack2.push(0);
        }else{
            stack.push(value);
            if(value < (int)stack.get((int)stack2.lastElement())){      //如果新输入的元素更小
                stack2.push(stack.size()-1);
            }
        }

    }

    public static void main(String[] args) {
        Stack<Integer> stack1 = new Stack<>();
        Stack<Integer> stack2 = new Stack<>();
        StackMinValue.init(stack1,stack2);
        System.out.println(get_min(stack1, stack2));
        StackMinValue.pop(stack1,stack2);
        System.out.println(get_min(stack1, stack2));
    }
}
/*
4
4
9
7
3
 */

求最大公约数

package 小灰灰;

/**
 * 求最大公约数
 */
public class Gcd {

    //辗转相除法，两个数a,b(a>b)的最大公约数等于a/b的余数和b的最大公约数，依赖递归，当两个数能够整数，或者一方为1
    //终止
    public int solution1(int a, int b) {
        int temp = 0;

        int num = 1;
        while (true) {
            if (a < b) {
                temp = a;
                a = b;
                b = temp;
            }
            if (a % b == 0) {
                num = b;
                break;
            }
            if (b == 1) {
                num = 1;
                break;
            }
            a = a % b;
        }
        return num;
    }

    //更相减损术，两个数a,b(a>b)的最大公约数等于a-b和b的最大公约数，依赖递归，当两个数相等便是最大公约数
    public int solution2(int a, int b) {
        int num = 1;
        int temp = 0;

        while (true) {
            if (a < b) {
                temp = a;
                a = b;
                b = temp;
            }
            if (a == b) {
                num = a;
                break;
            }
            a = a - b;
        }

        return num;
    }


    /**
     * 更相减和移位相结合算法：将辗转相除法和更相减算法结合起来，在更相减损数的基础上使用移位算法getGreatestCommonDivisor 简称gcd
     * 当a和b均为偶数时，gcd(a,b) = 2*gcd(a/2,b/2) = 2*gcd(a>>1,b>>1);
     * 当a为偶数，b为奇数时 gcd(a,b) = gcd(a/2,b) = gcd(a>>1,b)
     * 当a为奇数，b为偶数时 gcd(a,b) = gcd(a,b/2)=gcd(a,b>>1)
     * 当a和b均为奇数时，先利用更相减损术运算一次，gcd(a,b) = gcd(b,a-b),此时a-b必然时偶数，然后又可以使用移位运算
     * 特点：避免了取模运算，而且算法稳定，时间复杂度为O(log(max(a,b)))
     */

    public int solution3(int a, int b) {
        int temp =0;
        if(a<b){
            temp = a;
            a = b;
            b = temp;
        }

        if (a == b) return b;
        else if ((a & 1) == 0 && (b & 1) == 0)
            return 2*solution3(a>>1, b>>1);
        else if ((a & 1) == 1 && (b & 1) == 1){
            return solution3(b,a-b);
        }
        else if((a&1)==0 && (b&1)==1){
            return solution3(a>>1,b);
        }
        else{
            return solution3(a,b>>1);
        }
    }

    public static void main(String[] args) {
        Gcd gcd = new Gcd();
        int a = 100;
        int b = 44;
        System.out.println(gcd.solution1(a, b));
        System.out.println(gcd.solution2(a, b));
        System.out.println(gcd.solution3(a, b));
    }
}

栈实现队列

package 小灰灰;

import java.util.Stack;

//用栈来模拟队列
public class StackAsQueen {

    /**
     * 一个栈用来入栈，存数据，另一个栈来出栈，当出栈的栈内没有数据时，可以从进栈的栈内数据转到出栈的栈内
     * @param args
     */

    public static void push(Stack stack, int value){
        stack.push(value);
    }
    public static int pop(Stack stack, Stack stack2){
        if(stack2.size()==0){
            while (true){
               if(stack.isEmpty()==false){
                   int pop = (int) stack.pop();
                   stack2.push(pop);
               }else{
                   break;
               }
            }
        }
        return (int)stack2.pop();
    }

    public static void main(String[] args) {
        Stack<Integer> input = new Stack<>();
        Stack<Integer> output = new Stack<>();

        StackAsQueen.push(input,1);
        StackAsQueen.push(input,2);
        StackAsQueen.push(input,3);
        System.out.println(StackAsQueen.pop(input,output));
        System.out.println(StackAsQueen.pop(input,output));

        StackAsQueen.push(input,11);
        StackAsQueen.push(input,22);
        StackAsQueen.push(input,33);
        System.out.println(StackAsQueen.pop(input,output));
        System.out.println(StackAsQueen.pop(input,output));
    }
}

全排列和求全排列下一个数

package 小灰灰;

import java.util.Arrays;

/**
 * 全排列
 */
public class Perm {
    void Permutation(int a[], int m, int n) {   //递归实现全排列，四个数的全排列转成三个数的全排列，依次类推，直到一个数
        if (m == n) {
            System.out.print(Arrays.toString(a));
            System.out.println();
        } else {
            for (int i = m; i < n; i++) {
                int temp = a[i];
                a[i] = a[m];
                a[m] = temp;
                Permutation(a, m + 1, n);
                temp = a[i];
                a[i] = a[m];
                a[m] = temp;
            }
        }
    }

    //计算当前序列的全排列对应的一下个元素（如12543下一个元素为13245）,分为下面三个步骤，
    //1:从后向前查看逆序，找到逆序区域的前一位，也就是数字置换的边界。如124逆序前一位是2,143逆序前一位是1
    //2:从逆序区域里面选择大于置换边界的最小值进行交换
    //3:从置换区域后面的区域进行从小到大重排列
    void next(int value) {

        String nums = String.valueOf(value);
        int a[] = new int[nums.length()];
        for (int i = 0; i < nums.length(); i++) {
            a[i] = nums.charAt(i) - '0';
        }
        int index = 0; //用来计算逆序区域的下标
        for (int i = a.length - 1; i > 0; i--) {
            if (a[i] <= a[i - 1]) {
                continue;
            } else {
                index = i - 1;
                break;
            }
        }

        int num = Integer.MAX_VALUE;   //获取逆序区域的大于交换值的最小值
        int numIndex = a.length - 1;   //获取逆序区域的大于交换值的最小值对应的下标

        for (int i = a.length - 1; i > index; i--) {
            if (a[i] > a[index] && a[i] < num) {
                num = a[i];
                numIndex = i;
            }
        }
        int temp = a[index];
        a[index] = a[numIndex];
        a[numIndex] = temp;


        //对交换后的逆序区域进行重排序
        for (int i = index+1; i < a.length-1; i++) {
            for (int j = i ; j < a.length-1-(i-index-1); j++) {
                if(a[j] > a[j+1]){
                    int temps = a[j];
                    a[j] = a[j+1];
                    a[j+1] = temps;
                }
            }
        }

        System.out.println(Arrays.toString(a));
    }


    public static void main(String[] args) {
        Perm perm = new Perm();
        int a[] = {1, 2, 3, 4};
        perm.Permutation(a, 0, 4);
        System.out.println("======================");
        perm.next(1324);


    }
}

删去k个数字后的最小值

package 小灰灰;

import java.util.Arrays;
import java.util.concurrent.ForkJoinPool;

//删除k个数字后的最小值
public class KMin {
    //一个整数，删除k位后，使得新的整数最小。思路是从前往后删，因为前面的数位权重大，同时删除后保证最小就得优先删除大的数字。
    //对删除一位后的数字重新从头开始删除，删除数字的特点应该是出现逆序则删除，也就是前者比后者大，那么明显删除前者后新数字更小
    void delteleK(int num,int k){
        String str = String.valueOf(num);
        for (int i = 0; i < k; i++) {
            int index = 0;  //记录要删除数字的下标索引
            for (int j = 0; j < str.length()-1; j++) {
                if(str.charAt(j) > str.charAt(j+1)){
                    index = j;
                    break;
                }
            }

            str = str.substring(0,index) + str.substring(index+1,str.length());
        }

        System.out.println(str);
    }

    public static void main(String[] args) {
        KMin kMin = new KMin();
        kMin.delteleK(541270936,3);
    }
}

求两个数组的中位数

package 小灰灰;

//获取中间值，对于两个数组，希望获取两个数组组成的所有数字的中间大小的值

/**
 * 假设数组A的长度是m，绿色和橙色元素的分界点是i，数组B的长度是n，绿色和橙色元素的分界点是j，那么为了让大数组的左右两部分长度相等，则i和j需要符合如下两个条件：
 * i + j = （m+n+1）/2
 * （之所以m+n后面要再加1，是为了应对大数组长度为奇数的情况）
 * Max(A[i-1],B[j-1]) < Min(A[i], B[j])
 *
 * (直白的说，就是最大的绿色元素小于最小的橙色元素)
 * 由于m+n的值是恒定的，所以我们只要确定一个合适的i，就可以确定j，从而找到大数组左半部分和右半部分的分界，也就找到了归并之后大数组的中位数。
 * 要分析数组长度为1或者某些数组值明显大于或者小于另一个数组的情况
 */
public class MiddleNum {

    public static int getMax(int a, int b) {
        if (a >= b) return a;
        else return b;
    }

    public static int getMin(int a, int b) {
        if (a <= b) return a;
        else return b;
    }

    public static void num(int a[], int b[]) {
        int m = a.length;
        int n = b.length;
        int i = m / 2;
        int j = (m + n + 1) / 2 - i;  // 保证满足条件 i +j == （m+n+1）/2
        if (i == 0) {  //i=1开始，也就是至少指向第一个元素
            i++;
        }
        if (j == 0) { //j=1开始，也就是至少指向第一个元素
            j++;
        }
        while (true) {
            if (m > 1 && n > 1 && getMax(a[i - 1], b[j - 1]) <= getMin(a[i], b[j])) {
                break;
            }
            if (j > 1) {     //b长度大于1的情况
                if (a[i - 1] > b[j]) {   //数组a左部分最大值大于数组b右部分最小值
                    if (j == n) {   //数组b太小，
                        i = (m + n + 1) / 2 - j;
                        break;
                    } else if (i - 1 == 0) { //数组a最小值都很大
                        j = (m + n + 1) / 2 - i;
                        break;
                    } else { //调整
                        i--;
                        j++;
                    }
                }
            }
            if (j == 1) {  //考虑数组b长度只有1的特殊情况
                if (a[i - 1] > b[j - 1]) break;
                else {
                    i++;
                    j--;
                    break;
                }
            }
            if (i > 1) {   //a长度大于1的情况
                if (a[i] < b[j - 1]) {  //数组b左部分最大值大于数组a右部分最小值
                    if (i == m) {     //数组a太小
                        j = (m + n + 1) / 2 - i;
                        break;
                    } else if (j - 1 == 0) {  //数组b都很大
                        i = (m + n + 1) / 2 - j;
                        break;
                    } else {  //调整
                        i++;
                        j--;
                    }
                }
            }
            if (i == 1) {  //考虑数组a长度只有1的特殊情况
                if (a[i - 1] < b[j - 1]) break;
                else {
                    i--;
                    j++;
                }
            }
        }

        System.out.println(i + " " + j);
        if ((m + n) % 2 == 0) {
            if (a[i - 1] > b[j - 1] && j == n) System.out.println((a[i - 1] + a[i]) / 2.0); //数组b很小
            if (a[i - 1] > b[j - 1] && j < n) System.out.println((a[i - 1] + b[j]) / 2.0);
            if (a[i - 1] <= b[j - 1] && i == m) System.out.println((b[j - 1] + b[j]) / 2.0);  //数组a很小，直接在b找中值
            if (a[i - 1] <= b[j - 1] && i < m) System.out.println((a[i] + b[j - 1]) / 2.0);
        } else {
            if (a[i - 1] >= b[j - 1] && i > 1) System.out.println((a[i - 1]));
            if (a[i - 1] >= b[j - 1] && i == 1) System.out.println((b[j])); //数组a只有一个指标
            if (a[i - 1] < b[j - 1] && j == 1) System.out.println(a[i]);  //数组b只有一个值
            if (a[i - 1] < b[j - 1] && j > 1) System.out.println(b[j - 1]);
        }
    }


    public static void main(String[] args) {
        int a[] = {1, 3, 5, 7, 9, 11};
        int b[] = {2};
        MiddleNum.num(a, b);
    }
}

0-1背包

package 小灰灰;

import com.sun.glass.ui.View;

import java.util.Arrays;

/**
 * 0-1背包问题。
 * https://www.cnblogs.com/henuliulei/p/10041737.html
 * 核心点就是理解公式(1)和（2）:  (1)  V(i,j)=V(i-1,j)   j<W(i)该公式表明当前背包剩余容量装不下当前物品
 * （2）  V(i,j)=max(V(i-1,j),V(i-1,j-w[i])+v[i])    j>=W(i)该公式表明装入物品如果占用空间过多带来的价值少则选择不装入，否则装入
 * 最后根据V(i,j)>V(i-1,j)判断物品i是否装入和j=j-W[i]进行遍历数组V得到所有被装入的物品
 */
public class Packet_01 {
    public static void get_packet(int w[],int v[],int X[],int capacity){
        int maxValue = 0;
        int V[][] = new int[w.length+1][capacity+1];  //价值数组

        for (int i = 0; i < w.length+1; i++) {
            for (int j = 0; j < capacity+1; j++) {
                V[i][j] = 0;
            }
        }

        for (int i = 1; i < w.length+1; i++) {
            for (int j = 1; j < capacity+1; j++) {
                if(j<w[i-1]) V[i][j] = V[i-1][j];
                else V[i][j] = Math.max(V[i-1][j],V[i-1][j-w[i-1]]+v[i-1]);
            }
        }

        int capacity_index = capacity;
        for (int i = w.length; i >0 ; i--) {
            if(V[i][capacity] > V[i-1][capacity])
            {
                X[i-1] = 1;
                capacity -= w[i-1];
            }
            else{
                X[i-1] = 0;
            }
        }

        maxValue = V[w.length][capacity_index];

        System.out.println("装入情况为:"+ Arrays.toString(X));
        System.out.println("背包最大价值为:"+ maxValue);


    }

    public static void main(String[] args) {
        int w[] = {2,2,6,5,4};      //物品重量
        int v[] = {6,3,5,4,6};      //物品对应的价值
        int X[] = new int[w.length];    //物品是否被装入，默认0不装入，1装入
        Arrays.fill(X,0);
        Packet_01.get_packet(w,v,X,10);
    }
}
/*
重量:2 2 6 5 4
价值:6 3 5 4 6
背包容量:10
 */

金矿问题

package 小灰灰;

import java.util.Arrays;

/**
 * 金矿问题
 */
public class Gold {

    public static void getGold(int w[], int v[], int X[], int capacity) {
        int V[][] = new int[w.length + 1][capacity + 1];
        for (int i = 0; i < w.length + 1; i++) {
            for (int j = 0; j < capacity + 1; j++) {
                V[i][j] = 0;
            }
        }

        for (int i = 1; i < w.length + 1; i++) {
            for (int j = 1; j < capacity + 1; j++) {
                if(w[i-1] > j) V[i][j] = V[i-1][j];
                else V[i][j] = Math.max(V[i-1][j],V[i-1][j-w[i-1]]+v[i-1]);
            }
        }

        int capacityIndex = capacity;
        for (int i = w.length; i >0 ; i--) {
            if(V[i][capacityIndex] > V[i-1][capacityIndex]){
                X[i-1] = 1;
                capacityIndex =capacityIndex - w[i-1];
            }else{
                X[i-1] = 0;
            }
        }

        System.out.println("最大金矿获取价值为" + V[w.length][capacity]);
        System.out.println("最大金矿获取方案为" + Arrays.toString(X));

    }

    public static void main(String[] args) {
        int w[] = {3, 4, 3, 5, 5};  //每个金矿的人力需求
        int v[] = {200, 300, 350, 400, 500};   //金矿的产出
        int X[] = {0, 0, 0, 0, 0}; //记录金矿的选择
        int capacity = 10; //人力总量
        getGold(w,v,X,capacity);
    }

}
/*
w: 3,4,3,5,5
v: 200,300,350,400,500
 */

判断一个数是2的整数次幂

package 小灰灰;


import java.util.Scanner;

public class Bin {
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        int next = scanner.nextInt();
        System.out.println(next&(next-1));
        int num = next&(next-1);        //1000 & 000 == 0   ||| 101 & 100 == 100
        if(num==0){
            System.out.println("这个数是2的整数次幂");
        }
    }
}

寻找缺失的整数

package 小灰灰;

import java.util.Arrays;

//对于一个无序数组，里面有两个数只出现一次，其余的数出现偶数次，用最优的方案求出这两个只出现一次的两个数，
//直接暴力排序找数的话时间复杂度可以降到o(n)，如计数排序
//或者所有的数进行异或，相同的异或结果为0,0和任何数异或得任何数，不同的数异或结果为1的位置，这两个数必然在该位置上一个为0一个为1，按照这个规则分类进行xor，可以分别求出分类结果。
public class LackNum {

    public void solution1(int a[]){   //空间复杂度很低o(n)，但是额外开辟了空间
        Arrays.sort(a);
        int min = a[0];
        int max = a[a.length-1];
        int ano[] = new int[max-min+1];
        for (int i = 0; i < a.length; i++) {
            ano[a[i]-min] ++;
        }
        for (int i = 0; i < ano.length; i++) {
            if(ano[i] ==1) System.out.println(i+min);
        }
    }

    public int  judge(String str,int index){//判断倒数第index位置是否为1
        int shortNum = 0;
        if(str.length() <16){
            shortNum = 16-str.length();
            for (int i = 0; i < shortNum; i++) {
                str = "0"+str;
            }
        }
        if(str.charAt(str.length()-1-index) == '1') return 1;
        else return 0;
    }
    public void solution2(int a[]){  //先异或找到这两个数不同的位，然后按照该位分成两类进行异或便可分别求出这两个数
        int m = a[0];
        for (int i = 1; i < a.length; i++) {
            m^=a[i];
        }
        String str  = Integer.toBinaryString(m);
        System.out.println(str);
        int index = 0;
        for (int i = str.length()-1; i >=0 ; i--) {
            if(str.charAt(i)=='1') break;
            index ++;
        }

        int num1=-999;
        int num2=-999;
        for (int i = 0; i < a.length; i++) {
            String s = Integer.toBinaryString(a[i]);
            if(judge(s,index)==1){
                if(num1==-999){
                    num1 = a[i];
                }else{
                    num1 ^= a[i];
                }
            }else{
                if(num2 == -999){
                    num2 = a[i];
                }else{
                    num2 ^= a[i];
                }
            }
        }
        System.out.println(num1);
        System.out.println(num2);

    }

    public static void main(String[] args) {
        int a[] = {2,2,55,55,3,77,21,21,1,1,14,43,14,43};    // 3   77 只出现一次
        LackNum lackNum = new LackNum();
        lackNum.solution1(a);
        lackNum.solution2(a);

    }
}