hdu5375 Gray code

Problem Description

The reflected binary code, also known as Gray code after Frank Gray, is a binary numeral system where two successive values differ in only onebit (binary digit). The reflected binary code was originally designed to prevent spurious output from electromechanical switches. Today, Gray codes are widely used to facilitate error correction in digital communications such as digital terrestrial television and some cable TV systems.



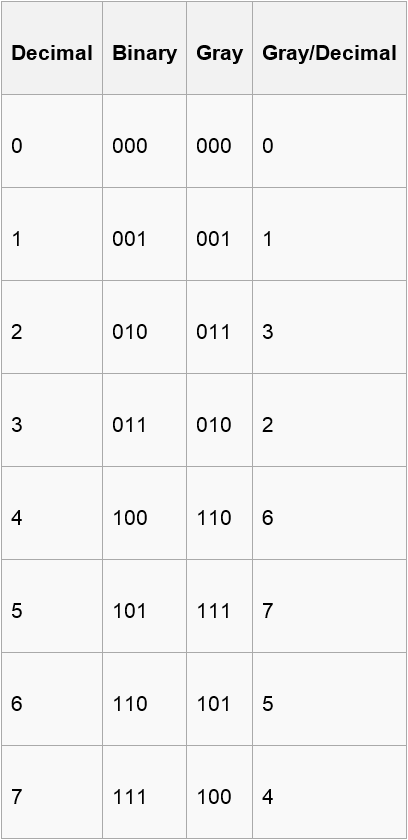
Now , you are given a binary number of length n including ‘0’ , ’1’ and ‘?’(? means that you can use either 0 or 1 to fill this position) and n integers(a1,a2,….,an) . A certain binary number corresponds to a gray code only. If the ith bit of this gray code is 1,you can get the point ai.
Can you tell me how many points you can get at most?

For instance, the binary number “00?0” may be “0000” or “0010”,and the corresponding gray code are “0000” or “0011”.You can choose “0000” getting nothing or “0011” getting the point a3 and a4.

 

Input

The first line of the input contains the number of test cases T.

Each test case begins with string with ‘0’,’1’ and ‘?’.

The next line contains n (1<=n<=200000) integers (n is the length of the string).

a1 a2 a3 … an (1<=ai<=1000)

 

Output

For each test case, output “Case #x: ans”, in which x is the case number counted from one,’ans’ is the points you can get at most

 

Sample Input

2 00?0 1 2 4 8 ???? 1 2 4 8

 

Sample Output

Case #1: 12

Case #2: 15

Gray码的运算是i^(i>>1)，给你每个位所对应的价值以及这个数（含0,1，？），？可以为0，也可以为1，求最大的价值，是一道dp题。

dp[i][1]表示第i为1时能产生的最大价值，dp[i][0]表示第i为时能产生的最大价值。

#include<iostream>
#include<stdio.h>
#include<stdlib.h>
#include<string.h>
#include<math.h>
#include<vector>
#include<map>
#include<set>
#include<queue>
#include<stack>
#include<string>
#include<algorithm>
using namespace std;
#define inf 88888888
#define maxn 200050
char s[maxn];
int dp[maxn][2],a[maxn];
int main()
{
	int n,m,i,j,T,len,num1=0;
	scanf("%d",&T);
	while(T--)
	{
		scanf("%s",s+1);
		len=strlen(s+1);
		for(i=1;i<=len;i++){
			scanf("%d",&a[i]);
		}
		dp[1][0]=dp[1][1]=-inf;
		if(s[1]=='1'){
			dp[1][1]=a[1];
		}
		if(s[1]=='0'){
			dp[1][0]=0;
		}
		if(s[1]=='?'){
			dp[1][0]=0;dp[1][1]=a[1];
		}
		
		for(i=2;i<=len;i++){
			dp[i][0]=dp[i][1]=-inf;
			if(s[i]=='1' || s[i]=='?'){
				dp[i][1]=max(dp[i-1][0]+a[i],dp[i-1][1]);
			}
			if(s[i]=='0' || s[i]=='?'){
				dp[i][0]=max(dp[i-1][0],dp[i-1][1]+a[i]);
			}
		}
		num1++;
		printf("Case #%d: %d
",num1,max(dp[len][0],dp[len][1]));
	}
	return 0;
}