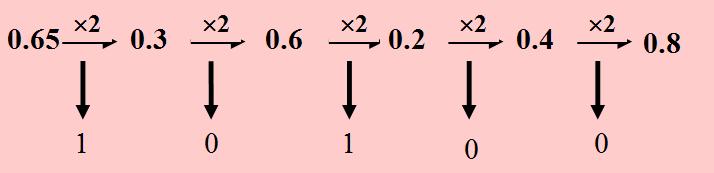今天翻了一本计算机基础的书籍,其中十进制、二进制、八进制、十六进制之间的转换挺有意思的,也容易犯糊涂,特温故而知新。
十进制数制系统
十进制数制系统包括 10 个数字:0、1、2、3、4、5、6、7、8、9
基为:10 逢十进一,如3+7=10,20+80=100
二进制数制系统
计算机中使用二进制表示数据
二进制包括两个符号:0和1
二进制逢二进一:(1+1)2=(10)2
二进制的基为2
示例:1000101100101101
八进制数制系统
用于缩短二进制的数字长度
八进制基是8,使用的符号为:0、1、2、3、4、5、6、7
逢八进一,即(7+1)8=(10)8
十六进制数制系统
十六进制数制系统的基是 16
十进制:0、1、2、3、4、5、6、7、8、9、10、11、12、13、14、15
十六进制:0、1、2、3、4、5、6、7、8、9、A、 B、 C、D、 E、 F
逢十六进一,如 (8+8)16=(10)16
示例:12B、00FFFF
计算机中以数量表示色彩
各数制的权
各种数制中不同位的权为“基的n-1次方(n为所在的位数)”。
如:
十进制中,各位的权为10n-1
二进制中,各位的权为2n-1
八进制中,各位的权为8n-1
十六进制中,各位的权为16n-1
数制转换
其他进制向十进制转换
十进制向其他进制转换
二进制、八进制、十六进制之间进行转化

非十进制转成十进制
方法:将相应进制的数按权展成多项式,按十进制求和。
(F8C.B)16
= F×162+8×161+C×160+B×16-1
= 3840+128+12+0.6875
=3980.6875
(10011.01)2
=1×24+0×23+0×22+1×21+1×20+0×2-1+1×2-2
=16+2+1+0.25
=19.25
整数部分的转换
除基取余法:用目标数制的基数去除十进制数,第一次相除所得余数为目的数的最低位 K0,将所得商再除以基数,反复执行上述过程,直到商为“0”,所得余数为目的数的最高位。
例:(81)10=(?)2
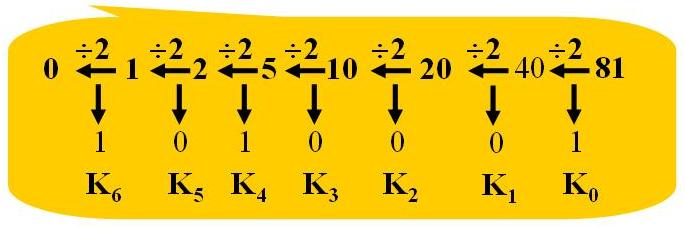
得:(81)10 =(1010001)2
小数部分的转换
乘基取整法:小数乘以目标数制的基数,第一次相乘结果的整数部分为目的数的最高位,将其小数部分再乘基数依次记下整数部分,反复进行下去,直到小数部分为“0”,或满足要求的精度为止。(如2-5,只要求到小数点后第五位)
例: (0.65)10 =( ? )2 要求精度为小数五位。
由此得:(0.65)10=(0.10100)2
综合得:(81.65)10=(1010001.10100)2
二进制与八进制间的转换
从小数点开始,将二进制数的整数和小数部分每三位分为一组,不足三位的分别在整数的最高位前和小数的最低位后加“0”补足,然后每组用等值的八进制码替代,即得目的数。
例:(11010111.0100111)2 = (327.234)8
二进制与十六进制间的转换
从小数点开始,将二进制数的整数和小数部分每四位分为一组,不足四位的分别在整数的最高位前和小数的最低位后加“0”补足,然后每组用等值的十六进制码替代,即得目的数。
例: (111011.10101)2=(3B.A8)16
综合示例:
将 -617 用八进制和十六进制(补码)表示:
答案: (-617)10=(176627)8=(fd97)16
原理:任何数在内存中都是以二进制补码的形式存放的.
正数的补码就是其本身的二进制.
负数的补码是其绝对值的二进制的反码加+1.
1:-617的绝对值:617
其二进制0000001001101001(整型16位)
2: 反码 :1111 1101 1001 0110.
3:加1后 :1111 1101 1001 0111.
转8进制,3位一体:
即:001 111 110 110 010 111
1 7 6 6 2 7
转16进制,4位一体:
即:1111 1101 1001 0111
F D 9 7