Sample Input
8 20 2
5 3
4 1
1 2
7 2
10 2
13 3
16 2
19 4
3 10 1
3 5
9 3
6 1
3 10 1
5 3
1 1
9 1
Sample Output
6
2
-1
题目大意:
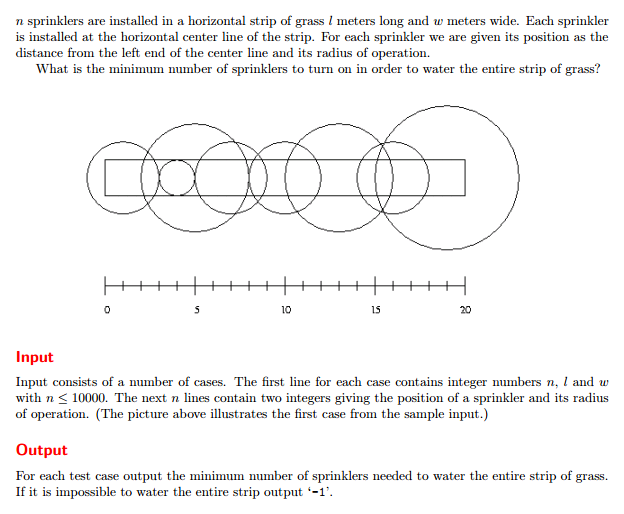
有一块草坪,长为l,宽为w,在它的水平中心线上有n个位置可以安装喷水装置,各个位置上的喷水装置的覆盖范围为以它们自己的半径ri为圆。求出最少需要的喷水装置个数。
分析与总结:
这题的关键在于转化
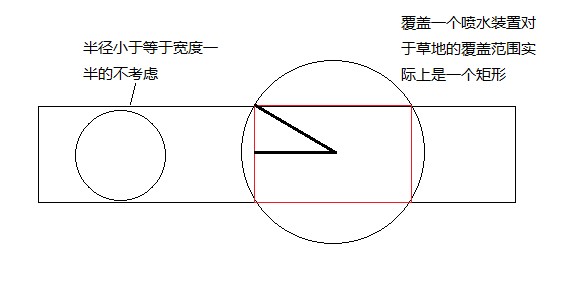
根据这图可以看出,一个喷水装置的有效覆盖范围就是圆中间的那个矩形。所以,在输入的同时,进行预处理,转换成矩形左边的坐标和右边的坐标。 这样,其实就转换成了经典的区间覆盖问题。
这题和我之前写的那道区域覆盖题基本是相同的。
AC代码:#include <stdio.h>
#include <string.h> #include <math.h> #include <algorithm> using namespace std; int n,f;; double l, w; double s, t; struct qujian { double start; double end; } ; qujian a[10005]; int cmp(qujian a,qujian b) { return a.end > b.end; } int main() { while (~scanf("%d%lf%lf", &n, &l, &w))
while (scanf("%d%lf%lf", &n, &l, &w)==3)
//在此,要加==3或者为~scanf(),不然会超时 { double start=0; f= 0; for (int i = 0; i < n; i ++) { scanf("%lf%lf", &s, &t); a[i].start = v - sqrt(r * r - w * w / 4); //开平方必须用double型,这里的式子是勾股定理 a[i].end = v + sqrt(r * r - w * w / 4); } sort(a,a+ n, cmp); while (start<l) { int i; for (i = 0; i < n; i ++) { if (a[i].start <=start&& a[i].end>start) { start=a[i].end; f++; break; } } if(i==n) break; } if (start<l) printf("-1 "); else printf("%d ",f); } return 0; }