支持向量机(三)——软间隔最大化 - 走看看

zoukankan html css js c++ java

支持向量机(三)——软间隔最大化
在支持向量机系列的前两篇中，介绍了一下完全线性可分向量机的构建过程，本篇将在此基础上介绍一下不完全线性可分的情况下实现支持向量机软间隔最大化过程。

1.线性分类时的两种情况

  情况一：

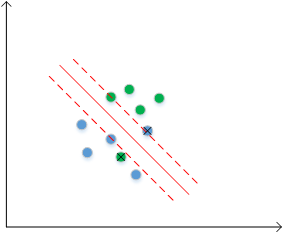
考虑下面这张图中的情况，这些数据点是完全线性可分的，蓝色点与绿色点两类，分割线为紫色实直线



如果按完全线性可分的情况考虑，也可以实现，但是这样得到的分类间隔(紫色虚线间距)比较小，换句话说就是分类准确率不够高，模型泛化能力不够。现在考虑这样一种做法，我们在建模时先不考虑其中一个绿色类点(带叉号的点)，然后对剩余的、完全线性可分的点创建最优分类超平面，这样就得到红色实线，而此时的分类间隔(红色虚线间距)就比之前大得多，我们也有理由相信此时得到的SVM泛化能力更好。

情况二：

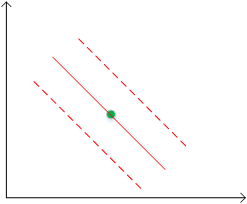
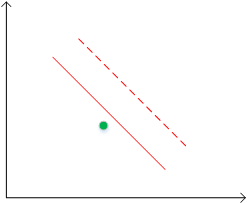
考虑下图中的这种情况，此时数据点不能完全线性可分

如果此时先不考虑带叉号的两个点，那么剩下的数据就完全线性可分了，我们可以找出红色实线那样的分类间隔。

2.软间隔最大化

对第1节中的两种情况，只要找出了影响最优分类超平面构建、“捣乱的数据点”(带叉号的点)，就可以解决我们的问题，所以我们要考虑将哪些点视为“捣乱的数据点”，在完全线性可分的情况下，所有的数据点均满足

   $y(w^{T}x+b)geq 1$

而在存在“捣乱数据点”的情况下，并不能保证所有的数据点满足上述等式，为此为每个数据点各自引入一个松弛变量 $xi$ ， $xi geq 0$ ，使其满足

   $y(w^{T}x+b)geq 1-xi$

很明显，如果 $xi$ 足够大，那么所有的数据点均满足上述等式条件了，所以此时需要考虑松弛变量的影响、调整优化目标函数

$min frac{1}{2}left | w ight |^{2}+Csum_{i=1}^{n}xi _{i}$

式中 $C$ 为惩罚参数，用于权衡 “ 最大化分类间隔距离 ” 和 “ 分类误差 ” ，一般在构建模型前确定， $C$ 越大，那么最终确定的分类间隔距离越小； $C$ 越小，那么最终确定的分类间隔距离越大。这样最终的优化问题表述如下

$min frac{1}{2}left | w ight |^{2}+Csum_{i=1}^{n}xi _{i}$

   $s.t. \, \, y_{i}(w^{T}x_{i}+b)geq 1-xi _{i}\, \, ,i=1,...,n$

   $xi _{i}geq 0\, \,,i=1,...,n$

3.优化计算过程

上面的优化问题，我们可以用拉格朗日乘子法建立函数

$F(w,b,xi ,lambda ,u)= frac{1}{2}left | w ight |^{2}+Csum_{i=1}^{n}xi _{i}-sum_{i=1}^{n}lambda _{i}(1-xi _{i}-y_{i}(w^{T}x_{i}+b))-sum_{i=1}^{n}u_{i}xi _{i}$

其中 $lambda _{i}geq 0$ ， $u _{i}geq 0$ ，在可行域范围内

$underset{lambda ,u}{max}\, \, F(w,b,xi, lambda,u)=frac{1}{2}left | w ight |^{2}+Csum_{i=1}^{n}xi _{i}$

因此我们的优化目标成了

$underset{w,b,xi }{min}\, \, underset{lambda ,u}{max}\, \, =frac{1}{2}left | w ight |^{2}+Csum_{i=1}^{n}xi _{i}-sum_{i=1}^{n}lambda _{i}(1-xi _{i}-y_{i}(w^{T}x_{i}+b))-sum_{i=1}^{n}u_{i}xi _{i}$

其对偶问题为

$underset{lambda ,u }{max}\, \, underset{w,b,xi}{min}\, \, =frac{1}{2}left | w ight |^{2}+Csum_{i=1}^{n}xi _{i}-sum_{i=1}^{n}lambda _{i}(1-xi _{i}-y_{i}(w^{T}x_{i}+b))-sum_{i=1}^{n}u_{i}xi _{i}$ (1)

由于这里的优化问题也是一个凸优化问题，满足Slater条件，因此可以求解对偶问题的解得到原优化问题的解。函数 $F(w,b,xi ,lambda ,u)$ 对 $w$ 、 $b$ 、 $xi$ 求偏导，并令其为0，得到

   $frac{partial F(w,b,xi ,lambda ,u)}{partial w}=0Rightarrow w=sum_{i=1}^{n}lambda _{i}y_{i}x_{i}$ (2)

   $frac{partial F(w,b,xi ,lambda ,u)}{partial b}=0Rightarrow sum_{i=1}^{n}lambda _{i}y_{i}=0$ (3)

$frac{partial F(w,b,xi ,lambda ,u)}{partial xi }=0Rightarrow C-lambda _{i}-u_{i}=0$ (4)

将式(2)、(3)、(4)代入式(1)中，得

   $underset{lambda }{max}\, \, sum_{i=1}^{n}lambda _{i}-frac{1}{2}sum_{i=1,j=1}^{n}lambda _{i}lambda _{j}y_{i}y_{j}x_{i}x_{j}$ (5)

   $s.t.\, \, sum_{i=1}^{n}lambda _{i}y_{i}=0$

$C-lambda_{i}-u_{i}=0$

$lambda_{i}geq 0$

$u_{i}geq 0$

非常有趣的是，式(5)与完全线性可分情况下的对偶优化目标完全一样，这说明，我们可以用处理不完全线性可分情况下的方法处理完全线性可分问题。由于目标函数中没有参数 $u_{i}$ ，因此可以将其消去，这样上述的目标函数及KKT条件可以写为如下

$underset{lambda }{min}\, \, frac{1}{2}sum_{i=1,j=1}^{n}lambda _{i}lambda _{j}y_{i}y_{j}x_{i}x_{j}-sum_{i=1}^{n}lambda _{i}$ (6)

   $s.t.\, \, sum_{i=1}^{n}lambda _{i}y_{i}=0$

$0leq lambda_{i}leq C$

到这里为止，利用训练数据集和预先设定的 $C$ 值，是可以解出最优解的，求解方法与线性完全可分情况下一致。

4.支撑向量问题

在上述的KKT条件中，由于 $0leq lambda_{i}leq C$ ，因此 $lambda _{i}$ 的取值对应着训练集中数据点不同的分类情况，下面来讨论一下这个问题。
- $lambda _{i}=0$
当 $lambda _{i}=0$ 时，依据 $C-lambda_{i}-u_{i}=0$ 的约束，可知 $u_{i}=C$ ，所以 $xi _{i}=0$ ， $y_{i}(w^{T}x_{i}+b)-1geq 0$ ，数据点被正确分类
- $0< lambda _{i}<C$
当 $0< lambda _{i}<C$ 时，依据 $C-lambda_{i}-u_{i}=0$ 的约束，可知 $0<u_{i}< C$ ，所以 $xi _{i}=0$ ， $y_{i}(w^{T}x_{i}+b)-1= 0$ ，此时数据点在分类边界上
- $lambda _{i}=C$
当 $lambda _{i}=C$ 时，依据 $C-lambda_{i}-u_{i}=0$ 的约束，可知 $u_{i}=0$ ，则此时 $xi_{i} geq 0$ ，而在 $y_{i}(w^{T}x_{i}+b)+xi_{i}-1=0$ 中， $xi_{i}$ 的取值影响着点的分类结果，所以有必要对 $xi_{i}$ 的取值情况分类讨论

1.> $xi _{i}=0$ ，此时 $y_{i}(w^{T}x_{i}+b)=1$ ，所以数据点在分类间隔边界上，并且被正确分类

2.> $0<xi _{i}<1$ ，此时 $0<y_{i}(w^{T}x_{i}+b)<1$ ，所以数据点在分类超平面与分类间隔边界之间，并且被正确分类



3.> $xi _{i}=1$ ， $y_{i}(w^{T}x_{i}+b)=0$ ，所以数据点在分类超平面上，无法被正确分类



  4.> $xi _{i}>1$ ， $y_{i}(w^{T}x_{i}+b)<0$ ，所以数据点在分类超平面的另一侧，被错误分类



在以上讨论的所有情况中，除 $lambda _{i}=0$ 及 $xi _{i}=1$ 的情况之外，其余情况下的数据点都是构成支持向量的点。

5.小结

本篇博文中讨论了不完全线性可分情况下支持向量机模型的构建问题，而其最终转化成的优化问题与完全线性可分情况下是一致的，这个结果让我们明白，当数据可以通过构建线性支持向量机实现分类时，我们不必知道数据是否是完全线性可分的，可以直接构建软间隔最大化支持向量机模型。
查看全文

相关阅读:
selenium--启动不同的浏览器
 selenium--文件下载
 selenium--常用的获取元素属性
 Python读取yaml文件
 python读Excel方法（xlrd）
Python--unittest框架
 Python--os模块
 git fork后提交pull request到原作者，别人的pull request我们要怎样merge融合
 GitHub fork的使用
 4.Factory Pattern（工厂模式）

原文地址：https://www.cnblogs.com/hgz-dm/p/10886214.html

Copyright © 2011-2022 走看看