说明
本文受知乎陈小米启发而写。有兴趣的朋友可以移步这里。
本文的代码完全是本人所撸。
问题描述
假想一个游戏。赢的概率是60%,输的概率40%。入场费随意交。如果赢了获得2倍的入场费金额(1赔1),输则输掉入场费。小米有1000元做本金,请问小米每次给多少入场费,理论上100次游戏后几何期望收益能最大?
【本人的疑问】为何这里考虑几何期望,而不是数学期望?【已解决,见代码注释!】
凯利公式
[f=p-frac{q}{b}
]
不多说,上代码。
完整代码
import pandas as pd
import numpy as np
import random
import matplotlib.pyplot as plt
'''
用蒙特卡罗方法,验证凯利公式的计算得到资金比例是不是最佳的
参考:https://zhuanlan.zhihu.com/p/20849995
'''
pwin = 0.6 # 胜率
b = 1 # 净赔率
# 凯利值
def kelly(pwin, b):
'''
参数
pwin 胜率
b 净赔率
返回
f 投注资金比例
'''
f = (b * pwin + pwin - 1) / b
return f
# 游戏
def play_game(f, cash=100, m=100):
global pwin, b
res = [cash]
for i in range(m):
if random.random() <= pwin:
res.append(res[-1] + int(f*res[-1])*b)
else:
res.append(res[-1] - int(f*res[-1]))
return res
# 蒙特卡罗方法重复玩游戏
def montecarlo(n=1000, f=0.15, cash=1000, m=100):
res = []
for i in range(n):
res.append(play_game(f, cash, m))
#return pd.DataFrame(res).sum(axis=0) / n #【 数学期望】不平滑
return np.exp(np.log(pd.DataFrame(res)).sum(axis=0) / n) # 【几何期望】平滑
n = 1000 # 重复次数
cash = 1000 # 初始资金池
m = 100 # 期数
f = 0.1 # 资金比例 10%
res1 = montecarlo(n, f, cash, m)
fk = kelly(pwin, b) # 资金比例 凯利值
res2 = montecarlo(n, fk, cash, m)
f = 0.5 # 资金比例 50%
res3 = montecarlo(n, f, cash, m)
f = 1.0 # 资金比例 100%
res4 = montecarlo(n, f, cash, m)
# 画个图看看
fig = plt.figure()
axes = fig.add_subplot(111)
axes.plot(res1,'r-',label='10%')
axes.plot(res2,'g*',label='{:.1%}'.format(fk))
axes.plot(res3,'b-',label='50%')
axes.plot(res4,'k-',label='100%')
plt.legend(loc = 0)
plt.show()
效果图
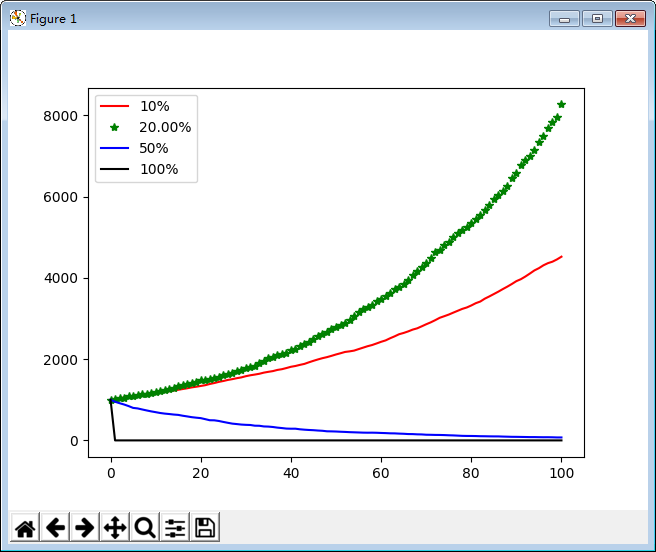
结论
由图显见,凯利值是最优的。