543. 二叉树的直径
给定一棵二叉树,你需要计算它的直径长度。一棵二叉树的直径长度是任意两个结点路径长度中的最大值。这条路径可能穿过也可能不穿过根结点。
示例 :
给定二叉树 1 / 2 3 / 4 5 返回 3, 它的长度是路径 [4,2,1,3] 或者 [5,2,1,3]。
思路:
分别统计左右子树的最大高度,把两个高度相加即是结果
1 class Solution { 2 public int diameterOfBinaryTree(TreeNode root) { 3 if(root == null){ 4 return 0; 5 } 6 // 分别统计左右子树的最大高度 7 int leftHeight = height(root.left); 8 int rihgtHeight = height(root.right); 9 10 // 把两个高度相加 11 return leftHeight + rihgtHeight; 12 } 13 14 // 统计树的高度 15 public int height(TreeNode root){ 16 if(root == null){ 17 return 0; 18 } 19 int leftHeight = height(root.left); 20 int rihgtHeight = height(root.right); 21 return Math.max(leftHeight, rihgtHeight) + 1; 22 } 23 }
运行结果,解答错误
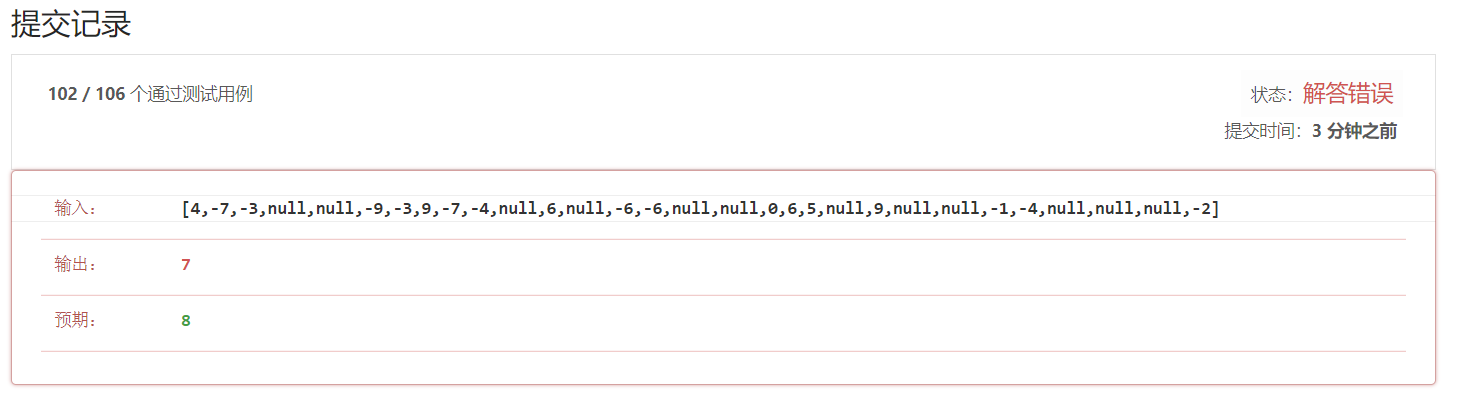
根据这个输入数据,建出下面这棵树,
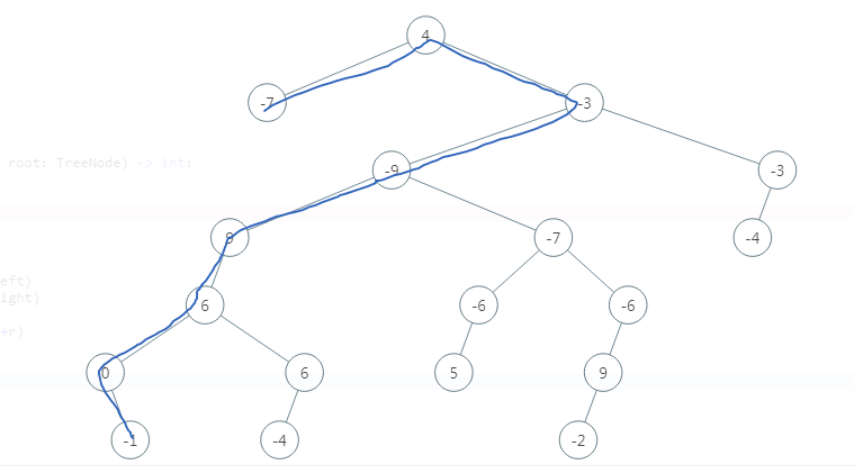
根据我们的理解,最大半径应该是上面这条路径,长度是7,但是答案给的预期是8,通过看题解发现可以另一条路径长度大于7,下面这条红色的路径就是长度大于7,为8
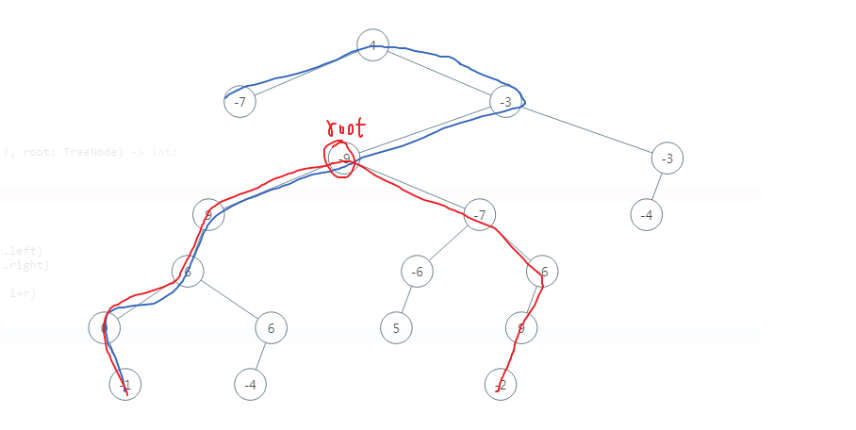
所以我们不能简单的统计root的左右子树的最大高度,而是应该统计每个结点的左右子树的最大高度之和,否则如果路径没有经过root结果就不能得出正确答案
下面是改正后的程序
1 class Solution { 2 public int max = 0; 3 public int diameterOfBinaryTree(TreeNode root) { 4 if(root == null){ 5 return 0; 6 } 7 height(root); 8 return max; 9 } 10 11 // 统计树的高度 12 public int height(TreeNode root){ 13 if(root == null){ 14 return 0; 15 } 16 int leftHeight = height(root.left); 17 int rightHeight = height(root.right); 18 // 更新最大半径 19 max = Math.max(max, leftHeight + rightHeight); 20 return Math.max(leftHeight, rightHeight) + 1; 21 } 22 }
力扣测试时间为0ms, 空间为39.6MB
复杂度分析:
时间复杂度:遍历了树的所有结点,所以时间复杂度为O(n)
空间复杂度:取决于递归层数,也就是树的高度,高度平均高度为O(logn), 所以空间平均复杂度为O(logn), 最大复杂度为O(n)