概览
- 基于模糊集二值分割
- 对比ostu等其他方法
- 模糊集图像聚类-FCM
- 对比KMeans聚类
- 人脸美颜
- 总结
摘要
模糊集理论,也称为模糊集合论,或简单地称为模糊集,1965年美国学者扎德在数学上创立了一种描述模糊现象的方法—模糊集合论。这种方法把待考察的对象及反映它的模糊概念作为一定的模糊集合,建立适当的隶属函数,通过模糊集合的有关运算和变换,对模糊对象进行分析。模糊集合论以模糊数学为基础,研究有关非精确的现象。客观世界中,大量存在着许多亦此亦彼的模糊现象。本文研究了基于模糊集图像分割在人脸美颜上的应用。要对人脸进行美颜,前提是要准确的定位到准确的部位,然后通过图像处理,得到想要的结果。本文先介绍了基于模糊集的二值分割和聚类,再介绍了如何将基于模糊集图像分割的方法应用到人脸美颜中。
关键词:(模糊集quad 二值分割quad 聚类分割 quad 人脸美颜)
模糊集二值分割
该算法是清华大学黄良凯(Liang-kai Huang) 所提出来的[1],因此国外一些论文里和代码里称之为Huang's fuzzy thresholding method。该论文结合了当时处于研究热潮的模糊集理论,提出了一种具有较好效果的图像二值化算法。
模糊集及其隶属度函数
设X代表一副大小为M×N的具有L个色阶的灰度图像,而(X_{mn})代表图像X中点(m, n)处的像素灰度值,定义(mu_X(x_{mn}))表示该点具有某种属性的隶属度值,也就是说我们定义了一个从图像X映射到[0,1]区间的模糊子集,用模糊集表达,即有:
其中 (0≤mu_X(x_{mn})≤1, m=0,1,...M-1, n=0,1,...N-1)。对于二值化来说,每个像素对于其所属的类别(前景或背景)都应该有很相近的关系,因此,我们可以这种关系来表示(mu_X(x_{mn}))的值。
定义H(g)表示图像中具有灰度级g的像素的个数,对于一个给定的阈值t,背景和前景各自色阶值的平均值(mu_0)和(mu_1)可用下式表示:
其中, L是色阶,一般的,取L=256。
上述(mu_0)和(mu_1),可以看成是指定阈值t所对应的前景和背景的目标值,而图像X中某一点和其所述的区域之间的关系,在直觉上应该和该点的色阶值与所属区域的目标值之间的差异相关。因此,对于点(m, n),我们提出如下的隶属度定义函数:
其中C是一个常数,该常数使得(0.5 leq mu_X(x_{mn}) leq 1)。因此,对于一个给定的阈值t,图像中任何一个像素要么属于背景,要么属于前景,因此,每个像素的隶属度不应小于0.5。C值在实际的编程中,可以用图像的最大灰度值减去最小灰度值来表达,即 (C=g_{max}-g_{min});
模糊度的度量及取阈值的规则
模糊度表示了一个模糊集的模糊程度,有好几种度量方式,本文使用了香农熵函数来度量模糊度。基于香农熵函数,一个模糊集A的熵定义为:
其中, 香农公式为:
拓展到二维,图像X的熵可以表示为:
因为灰度图像至多只有L个色阶,因此使用直方图式(1.7)可进一步写成:
E(X)具有以下属性:
(1). 0≤E(X)≤1 ;
(2). 如果(mu_x(X_{mn}) = 0)或者(mu_x(X_{mn}) = 1)时,E(X)具有最小值0,在本文中(mu_x(X_{mn}))只可能为1,此时分类具有最好的明确性。
(3). 当(mu_x(X_{mn}) = 0.5),E(X)获得最大值1,此时的分类具有最大的不明确性。
那么对于图像X,我们确定最好的阈值t的原则就是:对于所有的可能的阈值t,取香农熵值最小时的那个t为最终的分割阈值。
对比其他二值分割
OSTU二值分割算法是非常经典的算法。该算法假设一副图像由前景色和背景色组成,通过统计学的方法来选取一个阈值,使得这个阈值可以将前景色和背景色尽可能的分开。或者更准确的说是在某种判据下最优。与数理统计领域的 fisher 线性判别算法其实是等价的。但是, 当目标与背景的大小比例悬殊时,类间方差准则函数可能呈现双峰或多峰,此时效果不好。而模糊集二值分割在这个情况下分割效果更好。
从下图可以看出,模糊集二值分割效果更加好。
原图像

OSTU 本文方法


模糊集聚类图像分割
模糊聚类理论
聚类,就是将一组给定的未知类标号的样本分成内在的多个类别,使得同一类中的样本具有较高的相似度,而不同的类中样本差别大。 1973年,J.C. Bezdek提出了里程碑式的模糊C均值聚类算法(FCM)[2],通过引入样本到聚类中心的隶属度,使准则函数不仅可微,且软化了模式的归属。在众多模糊聚类算法中,FCM算法应用最广泛且较成功,它通过优化目标函数得到每个样本点对所有类中心的隶属度,从而决定样本点的类属以达到自动对样本数据进行分类的目的。
FCM算法原理
根据聚类的数目C和和一组包含N个数据的L维向量(X_k), 用FCM算法输出元素的隶属度(mu{ij}), 它表示数据(X_j)属于第 i 类的概率,通过求下面式子的目标函数的最小值得到,通常取m=2。
式(2.1)的约束条件为:
(2.1)式的约束条件下,可以求得目标函数取最小值时相应的隶属度矩阵和聚类中心。通常,该最小值用极小值代替,因此分别对各变量求偏导,并令偏导数为0,联立并解出更新后的模糊隶属度和聚类中心,如下公式(2.2)(2.3)。
FCM算法的步骤
- 设置目标函数的精度e,模糊指数m(m通常取2)和算法最大迭代次数;
- 初始化隶属度矩阵或聚类中心;
- 由式(2.2)(2.3)更新模糊划分矩阵和聚类中心;
- 若目标函数则迭代结束;否则,跳转执行第三步;
- 根据所得到的隶属度矩阵,取样本隶属度最大值所对应类作为样本聚类的结果,聚类结束。
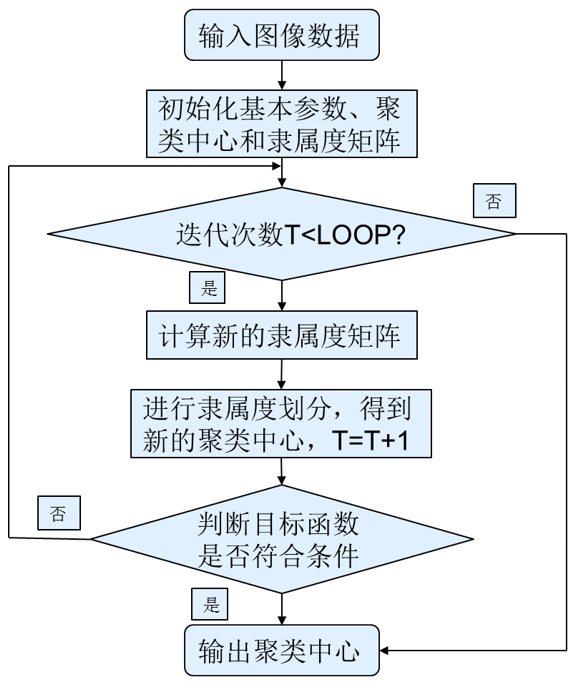
对比其他聚类方法
KMeans 本文方法


人脸美颜
由于人脸美颜过于复杂,因此我只研究了其中几个小方向。
- 肤色美白
- 肤色平滑
- 嘴唇亮化
特征区域的划分
首先对脸部特征区域进行模糊集图像分割。从分割的图像可以看出,人脸的皮肤还是比较完美的分割出来了,将人脸皮肤区域作为美白和平滑的模板。
然后使用双指数边缘保护肤色平滑[3]进行处理。美白和平滑程度的参数由人工输入。
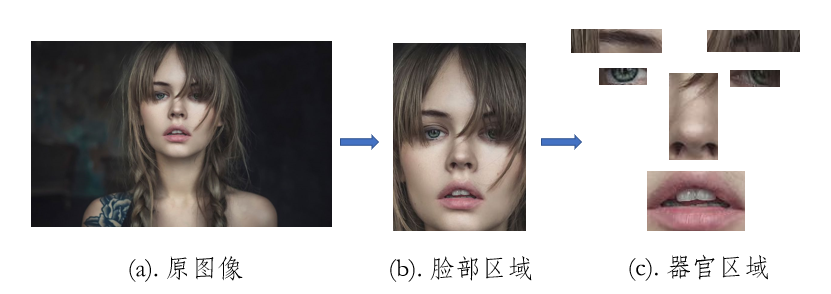
肤色美白和平滑
首先对脸部特征区域进行模糊集图像分割,然后使用双指数边缘保护肤色平滑[3]进行处理。
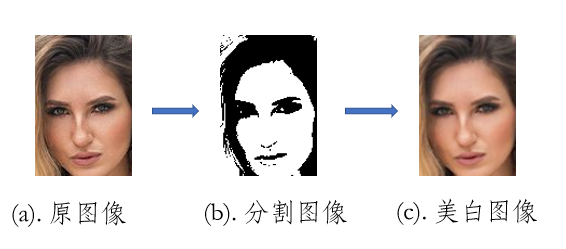
嘴唇亮化
首先对嘴部特征区域进行模糊集图像分割,然后在hsv颜色空间中进行颜色的亮化。亮化程度的参数由人工输入。
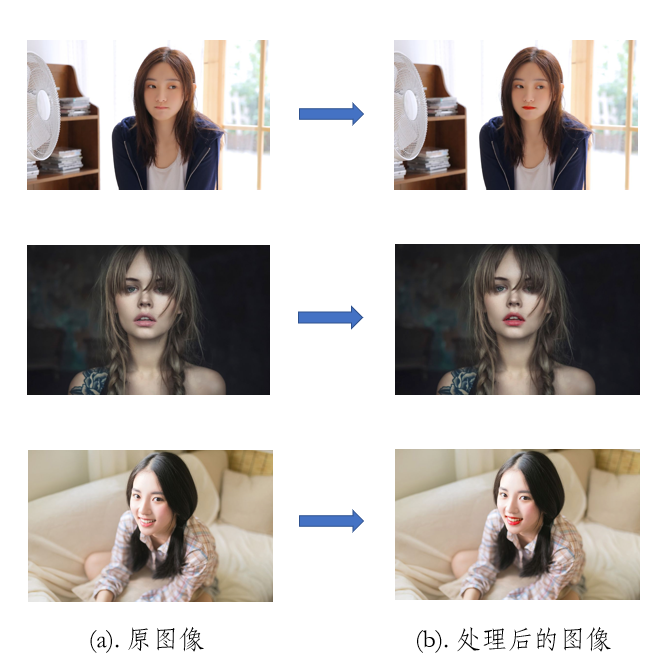
总结
本文研究了一种基于模糊集图像分割的快速人脸美颜的方法, 美化的图像符合人像美感的标准。本文方法通过模糊集图像分割方法,很好的分割出了皮肤、嘴唇等。在此基础之上,使用了常用的平滑和亮化方法, 得到了相对较好的美化效果。本文存在如下缺陷待改进,1.图像分割不能完美的将脸部皮肤分割出来,存在一些细节的地方不能分开;2.美白和亮化的程度是人工控制的参数,需要手动调节。
本文是将模糊集理论应用到人脸美颜的一次尝试,仍然存在很多地方有待改进。随着不确定性数学的发展,相信不确定性数学的应用场景会越来越丰富。
参考文献
本文章参考了如下文献。
[1]. LIANG-KAI HUANG and MAO-JIUN J. WANGt Department of Industrial Engineering, National Tsing Hua University, Hsinchu, Taiwan 300,R.O.C. Image thresholding by minimizing the measure of fuzziness
[2]. J.C. Bezdek, L.O. Hall, L.P. Clark, Review of MRsegmentation technique in pattern recognition[J], Medical Physics 10 (20) (1993) 33–48.
[3]. Qiu J L,Dai S K. Fast facial beautification algorithm based on skin-color segmentation and smoothness[J]. Journal of Image and Graph-ics,2016,21( 7) : 865-874.[邱佳梁,戴声奎 . 结合肤色分割与平滑的人脸图像快速美化[J]. 中国图象图形学报,2016,21( 7) : 865-874.][DOI:10. 11834 /jig. 20160704]
[4]. Li Zhenquan. Suitabilit y of fu zzy reasoning methods [ J]. Fuzzy Sets and System, 1998, 108( 3): 299-311.
[5]. LU Yi, CHEN Guang-meng, CHENG Song. Novel algorithm for image segmentation based on fuzzy set theory. Computer Engineering and Applications,2007,43(20):75-77.
[6]. 李磊,董卓莉,张德贤 . 基于自适应区域限制 FCM 的图像 分割方法[J].电子学报,2018,46(6):1312-1318.
[7]. 李亚峰 . 一种基于多字典学习的图像分割模糊方法[J]. 电子学报,2018,46(7):1700-1709.
[8]. Ahmed M N,Yamany S M,Mohamed N,et al.A modi-fied fuzzy c - means algorithm for bias field estimationand segmentation of MRI data[J].IEEE Trans on MedImaging,2002,21(3):193-199.