leetcode Linked List Cycle II

给定一个链表，如果有环，返回环的起点，如果没环，则返回空指针。

法一：unordered_set存做过的节点，一旦出现重复，那么它就是起点了。O(n)空间

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    ListNode *detectCycle(ListNode *head) {
        if (!head || !head->next) return NULL;
        unordered_set<ListNode *> uset;
        uset.insert(head);
        while(head -> next)
        {
            if (uset.count(head -> next))
                return head -> next;
            uset.insert(head -> next);
            head = head -> next;
        }
        return NULL;
    }
};

法二：我们想要在常数空间解决，那么就要分析一下图了。我直接参考这位大神的了：

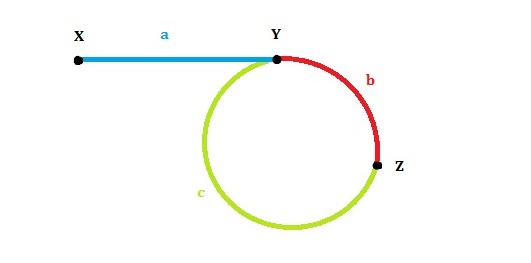
两个指针一个走一步，一个走两步，假设在环中Z相遇，那么一个从X开始走，一个从Z开始走，每次走一步，就会在Y相遇。返回Y就行了。

因为由两个指针速度知道2*(a+b) = a + b + c + b，那么a == c了，所以从X和Z出发就会在Y相遇了。

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    ListNode *detectCycle(ListNode *head) {
        if (!head || !head->next) return NULL;
        ListNode *l1, *l2, *l3, *l4;
        l1 = head; l2 = head;
        while(l1 && l2)
        {
            l1 = l1 -> next;
            l2 = l2 -> next;
            if (!l2)
                break;
            l2 = l2 -> next;
            if (l1 == l2)
                break;
        }
        if (!l1 || !l2)
            return NULL;
        l3 = head;
        while(1)
        {
            if (l3 == l1)
                return l1;
            l1 = l1 -> next;
            l3 = l3 -> next;
        }
    }
};