参考资料:机器学习课程的ppt……
Mixture Models
我们将研究混合模型,包括高斯混合模型和伯努利混合模型。
关键思想是引入潜变量,它允许从更简单的分布形成复杂的分布。·
我们将看到,混合模型可以用具有离散的潜在变量(在有向的图形模型中)来解释。
在后面的课堂上,我们还会看到连续的潜在变量。
K-Means Clustering
k-群集分析
首先,我们来看看下面的问题:在多维空间中识别数据点的簇或组。
我们希望把数据划分成K簇,其中给出k。
我们观察到由N维观测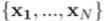 组成的数据集。
组成的数据集。
其次,我们介绍了D维向量,原型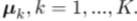 我们可以认为K代表聚类中心。
我们可以认为K代表聚类中心。

我们的目标是:找到数据点到集群的分配。-每个数据点到其最接近的原型的平方距离的总和是最小值。
·对于每个数据点xn,我们引入长度为K的二进制向量rn(K的1/K编码),它指示数据点xn被分配给哪个K簇。
定义目标(失真测度):
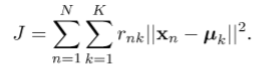
它表示每个数据点到其指定的原型k的距离的平方和。
我们的目标是找到rnk和聚类中心uk的值,以便最小化目标J。
Iterative Algorithm
定义迭代过程以最小化:
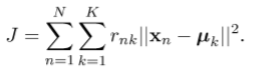
关于给定的k,将j相对于RNK(E步骤)最小化:
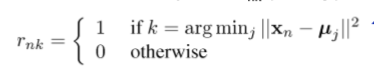
简单地说,将第n个数据点Xn分配到它最接近的集群中心。
给出给定的RNK,相对于k(m步骤)最小化J:
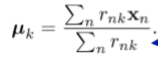 其中n是分配给群集K的点的数目。
其中n是分配给群集K的点的数目。
集合k等于分配给群集K的所有数据点的平均值。
保证了收敛到局部最小值(不是全局最小值)。
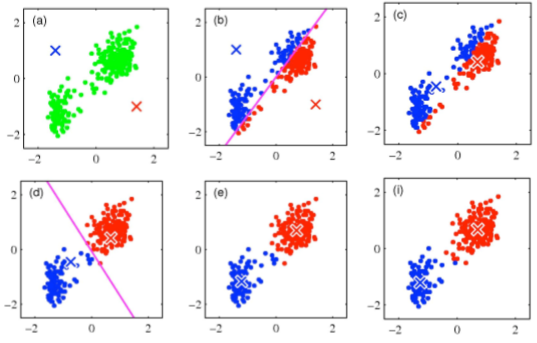
举例
在旧的数据集上使用k-均值(k=2)的例子,收敛步骤如下:
参考资料:
https://www.cnblogs.com/cfantaisie/archive/2011/08/20/2147075.html
matlab代码:
如果理解了上面的内容,写起来一小时内就可以完成,为何不自己试一试呢。
函数:
function [data, mu, var, weight] = CreateSample(M, dim, N)
% 生成实验样本集,由M组正态分布的数据构成
% % GMM模型的原理就是仅根据数据估计参数:每组正态分布的均值、方差,
% 以及每个正态分布函数在GMM的权重alpha。
% 在本函数中,这些参数均为随机生成,
%
% 输入
% M : 高斯函数个数
% dim : 数据维数
% N : 数据总个数
% 返回值
% data : dim-by-N, 每列为一个数据
% miu : dim-by-M, 每组样本的均值,由本函数随机生成
% var : 1-by-M, 均方差,由本函数随机生成
% weight: 1-by-M, 每组的权值,由本函数随机生成
% ----------------------------------------------------
%
% 随机生成不同组的方差、均值及权值
weight = rand(1,M);
weight = weight / norm(weight, 1); % 归一化,保证总合为1
var = double(mod(int16(rand(1,M)*100),10) + 1); % 均方差,取1~10之间,采用对角矩阵
mu = double(round(randn(dim,M)*100)); % 均值,可以有负数
for i = 1: M
if i ~= M
n(i) = floor(N*weight(i));
else
n(i) = N - sum(n);
end
end
% 以标准高斯分布生成样本值,并平移到各组相应均值和方差
start = 0;
for i=1:M
X = randn(dim, n(i));
X = X.* var(i) + repmat(mu(:,i),1,n(i));
data(:,(start+1):start+n(i)) = X;
start = start + n(i);
end
save('d:data.mat', 'data');
function [MU_pre,SIGMA_pre,Alpha_Pre,Center_Pre]=CreatePre(Gao_siNum,dimention); % 生成随机的MU,SIGMA和权重 % 输入 % Gao_siNum : 高斯函数个数 % dimention : 数据维数 % 返回值 % MU_pre : dim-Num, 每组样本的均值,由本函数随机生成 % SIGMA_pre : dim-M, 均方差,由本函数随机生成 % Alpha_Pre : 1-M, 权重 % Center_Pre : 2-M,每个点的中心 % ---------------------------------------------------- % MU_pre=normrnd(10,5,dimention,Gao_siNum); SIGMA_pre=normrnd(10,5,1,Gao_siNum); Alpha_Pre=normrnd(10,5,1,Gao_siNum); Center_Pre=normrnd(30,100,2,Gao_siNum); % MU_pre=normrnd(rand(1),rand(1),dimention,Gao_siNum); % SIGMA_pre=normrnd(rand(1),rand(1,1),dimention,Gao_siNum); % Alpha_Pre=normrnd(rand(1,1),rand(1,1),1,Gao_siNum);
主程序:
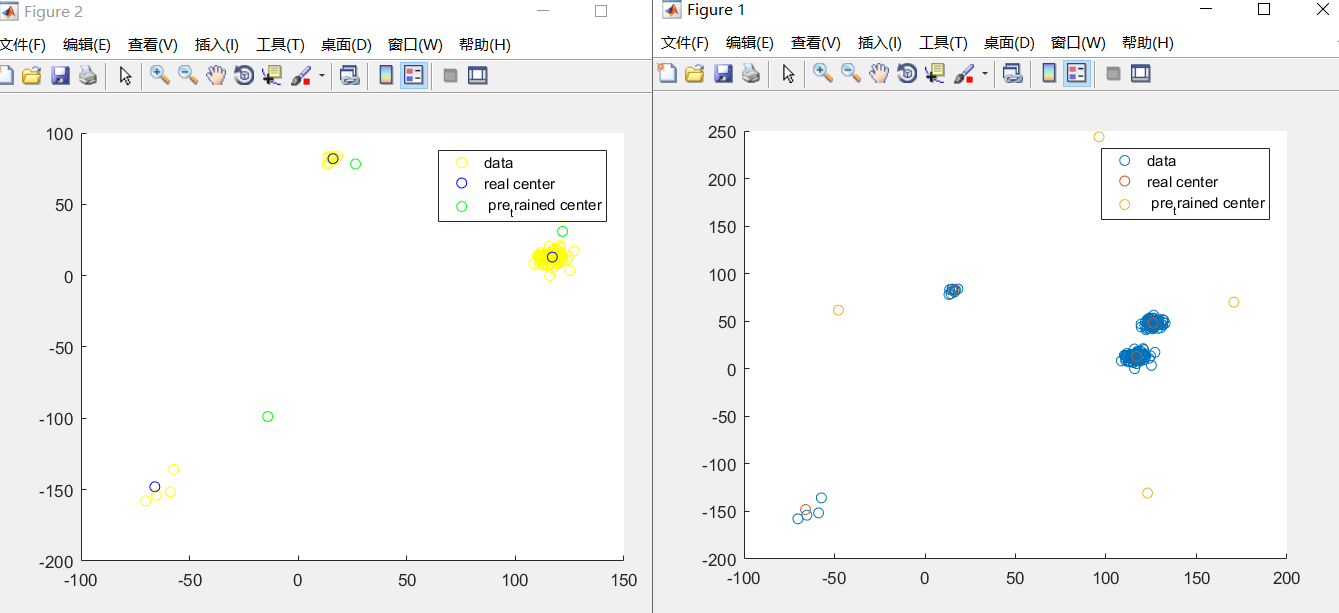
close all % %% 画图 % num=60;%每个集合的样本数 % x=1:1:num; % MU1=4; % MU2=6; % MU3=2; % SIGMA=2; % y1=normrnd(MU1,SIGMA,1,num); % y2=normrnd(MU2,SIGMA,1,num); % y3=normrnd(MU3,SIGMA,1,num); % %% 画出原图像 % figure(); % hold on % scatter(x,y1); % scatter(x,y2); % scatter(x,y3); % hold off %% 创建生成数据并且绘图 Gao_siNum=4; dimention=2; sampleNum=180; [data, MU, SIGMA, weight] = CreateSample(Gao_siNum, dimention, sampleNum); % 生成测试数据 draw_x=data(1,:);%x轴 draw_y=data(2,:);%y轴 figure(); scatter(draw_x,draw_y); hold on scatter(MU(1,:),MU(2,:)); hold off %% 进行区分GMM_EM算法 [MU_pre,SIGMA_pre,Alpha_Pre,Center_Pre]=CreatePre(Gao_siNum,dimention); hold on scatter(Center_Pre(1,:),Center_Pre(2,:)); legend('data','real center',' pre_trained center'); hold off %% EM 迭代停止条件 maxStep=2000; %% 初始化参数 [dim, N] = size(data); nbStep = 0; Epsilon = 0.0001; distance=zeros(Gao_siNum,sampleNum); distance_min=zeros(1,sampleNum); distance_min_Index=zeros(1,sampleNum); while (nbStep < 1200) nbStep=nbStep+1; %计算每个点到各自中心的衡量,需要一个dimention*sampleNum大小的矩阵来保存 for i=1:sampleNum for j=1:Gao_siNum %(x1-x2)^2+(y1-y2)^2 distance(j,i)=sqrt((data(1,i)-Center_Pre(1,j))^2+(data(2,i)-Center_Pre(2,j))^2); end end %% E-步骤 %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% for i=1:sampleNum distance_min(1,i)=min(distance(:,i)); for j=1:Gao_siNum if distance(j,i)==distance_min(1,i); distance_min_Index(1,i)=j;%将第n个数据点Xn分配到它最接近的集群中心。 end end end %% M-步骤 %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %给出给定的RNK,相对于k(m步骤)最小化J:重新贴标签 %先把每个类的对应标签找出来,然后再计算均值。 find_dimention1= find(distance_min_Index==1); %查找对应的类 find_dimention1(1)=1; n=length(find_dimention1); Center_Pre(1,1)=sum(data(1,find_dimention1))/n; Center_Pre(2,1)=sum(data(2,find_dimention1))/n; find_dimention2= find(distance_min_Index==2); %查找对应的类 find_dimention2(1)=1; n=length(find_dimention2); Center_Pre(1,2)=sum(data(1,find_dimention2))/n; Center_Pre(2,2)=sum(data(2,find_dimention2))/n; find_dimention3= find(distance_min_Index==3); %查找对应的类 find_dimention3(1)=1; n=length(find_dimention3); Center_Pre(1,3)=sum(data(1,find_dimention3))/n; Center_Pre(2,3)=sum(data(2,find_dimention3))/n; find_dimention4= find(distance_min_Index==4); %查找对应的类 n=length(find_dimention4); find_dimention4(1)=1; Center_Pre(1,4)=sum(data(1,find_dimention4))/n; Center_Pre(2,4)=sum(data(2,find_dimention4))/n; % for j=1:Gao_siNum % n=length(find_dimention(:,j)); % Center_Pre(1,j)=sum(data(1,find_dimention(:,j)))/n; % Center_Pre(2,j)=sum(data(2,find_dimention(:,j)))/n; % end %% cost=0; for j=1:Gao_siNum cost=cost+sum(distance(:,j)); end end %% figure(); hold on scatter(draw_x,draw_y,'y'); scatter(MU(1,:),MU(2,:),'b'); scatter(Center_Pre(1,:),Center_Pre(2,:),'g'); legend('data','real center',' pre_trained center'); hold off
成果: