原标题:LCT(Link-Cut Tree)详解(蒟蒻自留地)
出处:https://blog.csdn.net/saramanda/article/details/55253627
如果你还没有接触过LCT,你可以先看一看这里:
(看不懂没关系,先留个大概的印像)http://www.cnblogs.com/BLADEVIL/p/3510997.html
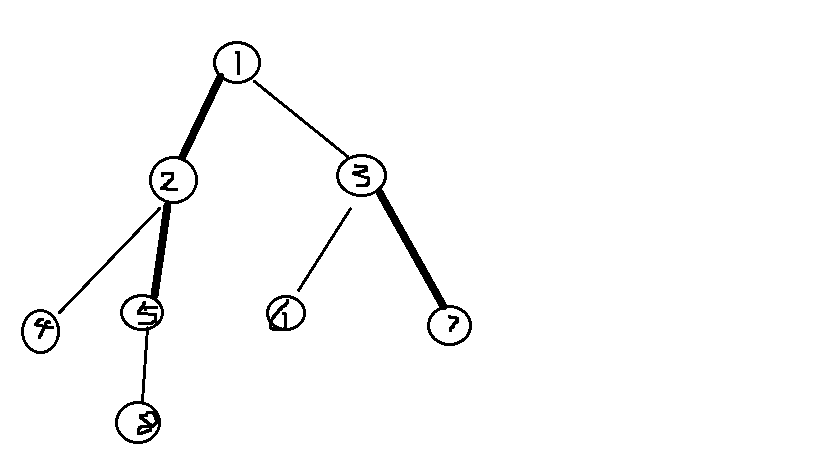
看完之后我们知道,LCT和静态的树链剖分很像。怎么说呢?这两种树形结构都是由若干条长度不等的“重链”和“轻边”构成(名字可以不同,大概就是这个意思),“重链”之间由”轻边”连接。就像这样:
可以想象为一棵树被人为的砍成了一段段。
LCT和树链剖分不同的是,树链剖分的链是不会变化的,所以可以很方便的用线段树维护。但是,既然是动态树,那么树的结构形态将会发生改变,所以我们要用更加灵活的维护区间的结构来对链进行维护,不难想到Splay可以胜任。如何分离树链也是保证时间效率的关键(链的数量和长度要平衡),树链剖分的“重儿子”就体现了前人博大精深的智慧。
在这里解释一下为什么要把树砍成一条条的链:我们可以在logn的时间内维护长度为n的区间(链),所以这样可以极大的提高树上操作的时间效率。在树链剖分中,我们把一条条链放到线段树上维护。但是LCT中,由于树的形态变化,所以用能够支持合并、分离、翻转等操作的Splay维护LCT的重链(注意,单独一个节点也算是一条重链)。
这时我们注意到,LCT中的轻边信息变得无法维护。为什么呢?因为Splay只维护了重链,没有维护重链之间的轻边;而LCT中甚至连根都可以不停的变化,所以也没法用点权表示它父边的边权(父亲在变化)。所以,如果在LCT中要维护边上信息,个人认为最方便的方法应该是把边变成一个新点和两条边。这样可以把边权的信息变成点权维护,同时为了不影响,把真正的树上节点的点权变成0,就可以用维护点的方式维护边。
LCT的各种操作:
LCT中用Splay维护链,这些Splay叫做“辅助树“。辅助树以它上面每个节点的深度为关键字维护,就是辅助树中每个节点左儿子的深度小于当前节点的深度,当前节点的深度小于右儿子的深度。
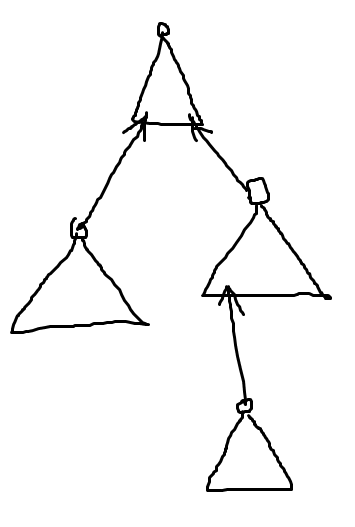
可以把LCT认为是一个由Splay组成的森林,就像这样:(三角形代表一棵Splay,对应着LCT上一条链)
箭头是什么意思呢?箭头记录着某棵Splay对应的链向上由轻边连着哪个节点,可以想象为箭头指向“Splay 的父亲”。但是,Splay的父亲并不记录有这个儿子,即箭头是单向的。同时,每个节点要记录它是否是它所在的Splay的根。这样,Splay构成的森林就建成了。
这个是我的Splay节点最基本的定义:(如果要维护更多信息就像Splay维护区间那样加上更多标记)
-
struct node{
-
int fa,ch[2]; //父亲和左右儿子。
-
bool reverse,is_root; //区间反转标记、是否是所在Splay的根
-
}T[maxn];
LCT中基本的Splay上操作:
-
int getson(int x){
-
return x==T[T[x].fa].ch[1];
-
}
-
void pushreverse(int x){
-
if(!x)return;
-
swap(T[x].ch[0],T[x].ch[1]);
-
T[x].reverse^=1;
-
}
-
void pushdown(int x){
-
if(T[x].reverse){
-
pushreverse(T[x].ch[0]);
-
pushreverse(T[x].ch[1]);
-
T[x].reverse=false;
-
}
-
}
-
void rotate(int x){
-
if(T[x].is_root)return;
-
int k=getson(x),fa=T[x].fa;
-
int fafa=T[fa].fa;
-
pushdown(fa);pushdown(x); //先要下传标记
-
T[fa].ch[k]=T[x].ch[k^1];
-
if(T[x].ch[k^1])T[T[x].ch[k^1]].fa=fa;
-
T[x].ch[k^1]=fa;
-
T[fa].fa=x;
-
T[x].fa=fafa;
-
if(!T[fa].is_root)T[fafa].ch[fa==T[fafa].ch[1]]=x;
-
else T[x].is_root=true,T[fa].is_root=false;
-
//update(fa);update(x); //如果维护了信息,就要更新节点
-
}
-
void push(int x){
-
if(!T[x].is_root)push(T[x].fa);
-
pushdown(x);
-
}
-
void Splay(int x){
-
push(x); //在Splay到根之前,必须先传完反转标记
-
for(int fa;!T[x].is_root;rotate(x)){
-
if(!T[fa=T[x].fa].is_root){
-
rotate((getson(x)==getson(fa))?fa:x);
-
}
-
}
-
}
access操作:
这是LCT最核心的操作。其他所有操作都要用到它。
他的含义是”访问某节点“。作用是:对于访问的节点x,打通一条从树根(真实的LCT树)到x的重链;如果x往下是重链,那么把x往下的重边改成轻边。可以理解为专门开辟一条x到根的路径,由一棵Splay维护这条路径。
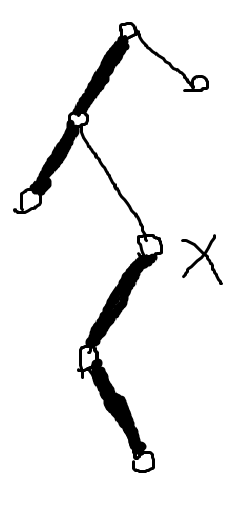
access之前:(粗的是重链) access之后:
access实现的方式很简单;
先把x旋转到所在Splay的根,然后把x的右孩子的is_root设为true(此时右孩子对应的是x下方的重链,这样就断开了x和下方的重链)。
用y记录上一次的x(初始化y=0),把y接到x的右孩子上,这样就把上一次的重链接到了当前重链一起,同时记得T[y].is_root=false。
记录y=x,然后x=T[x].fa,把x上提。重复上面的步骤直到x=0。
代码:
-
void access(int x){
-
int y=0;
-
do{
-
Splay(x);
-
T[T[x].ch[1]].is_root=true;
-
T[T[x].ch[1]=y].is_root=false;
-
//update(x); //如果维护了信息记得更新。
-
x=T[y=x].fa;
-
}while(x);
-
}
mroot操作:
这个操作的作用是把某个节点变成树根(这里的根指的是整棵LCT的根)。加上access操作,就可以方便的提取出LCT上两点之间的路径。提取u到v的路径只需要mroot(u),access(v),然后v所在的Splay对应的链就是u到v的路径。
mroot实现的方式:
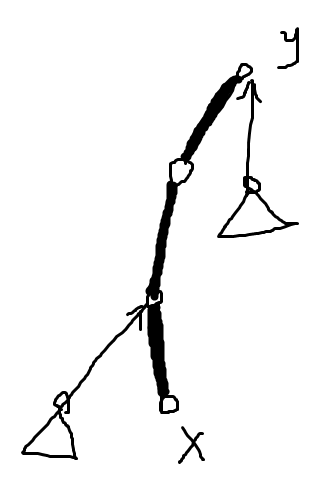
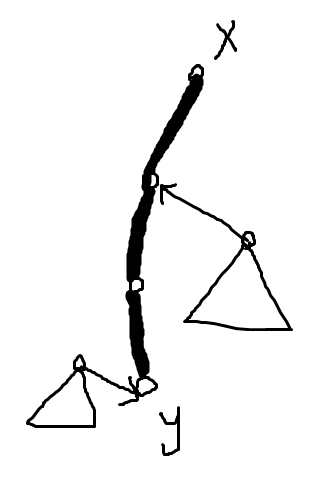
由于LCT是Splay组成的森林,所以要把x变成根就只需要让所有Splay的父亲最终指向x所在Splay。所以先access(x),Splay(x),把现在的根和将成为根的x链在一棵Splay中,并转到根即可。但是我们注意到,由于x成为了新的根,所以它和原来的根所在的Splay中深度作为关键字的性质遭到了破坏:新根x应该是Splay中深度最小的,但是之前的操作并不会改变x的深度(也就是目前x依旧是当前Splay中深度最深的)。所以,我们需要把所在的这棵Splay翻转过来。
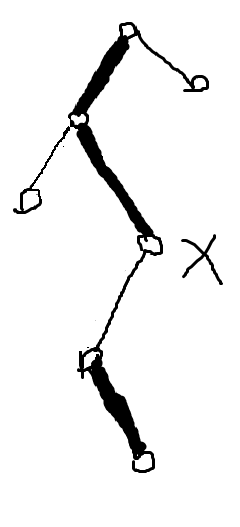
(粗的是重链,y是原来的根)
翻转前: 翻转后:
这时候x才真正变成了根。
代码:
-
void mroot(int x){
-
access(x);
-
Splay(x);
-
pushreverse(x);
-
}
link操作:
这个操作的作用是连接两棵LCT。对于link(u,v),表示连接u所在的LCT和v所在的LCT;
link实现的方式:
很简单,只需要先mroot(u),然后记录T[u].fa=v就可以了,就是把一个Splay森林连到另一个上。
代码:
-
void link(int u,int v){
-
mroot(u);
-
T[u].fa=v;
-
}
cut操作:
这个操作的作用是分离出两棵LCT。
代码:
-
void cut(int u,int v)
-
mroot(u); //先把u变成根
-
access(v);Splay(v); //连接u、v
-
pushdown(v); //先下传标记
-
T[u].fa=T[v].ch[0]=0;
-
//v的左孩子表示v上方相连的重链
-
//update(v); //记得维护信息
-
}
这些就是LCT的基本操作。我推荐几个LCT的练习题:
bzoj2049 SDOI2008洞穴勘探
模板题,只需要link和cut,然后询问连通性。题解:
http://blog.csdn.net/saramanda/article/details/55210235
bzoj2002 HNOI2010弹飞绵羊
模板题,需要link和询问某点到根的路径长度。题解:
http://blog.csdn.net/saramanda/article/details/55210418
bzoj3669 NOI2014魔法森林
LCT的综合应用。题解: