98.分形之城

原题链接：98. 分形之城

解题思路

递归+分治+数学坐标系公式+找规律

递归+分治好理解，因为这个题目中最显著的特点就是，不断地重复旋转复制，也就是N级城市，可以由4个N−1级城市构造，因此我们每次可以不断地分形N−1级，将问题范围不断地缩小即可
这道题目的数学坐标公式，其实一共有两个，一个是高中的数学函数，旋转，这是一个难点，其实可以通过找规律，求解，第二公式则是欧几里得距离公式。√(x1−x2)²−(y1−y2)²
最难的就是如何旋转这个正方形 找规律。

总的来说这道题目数学知识较多，考察画图能力，解法自然，数据毒瘤，相信可以给你的NOIP一个有利的一脚。

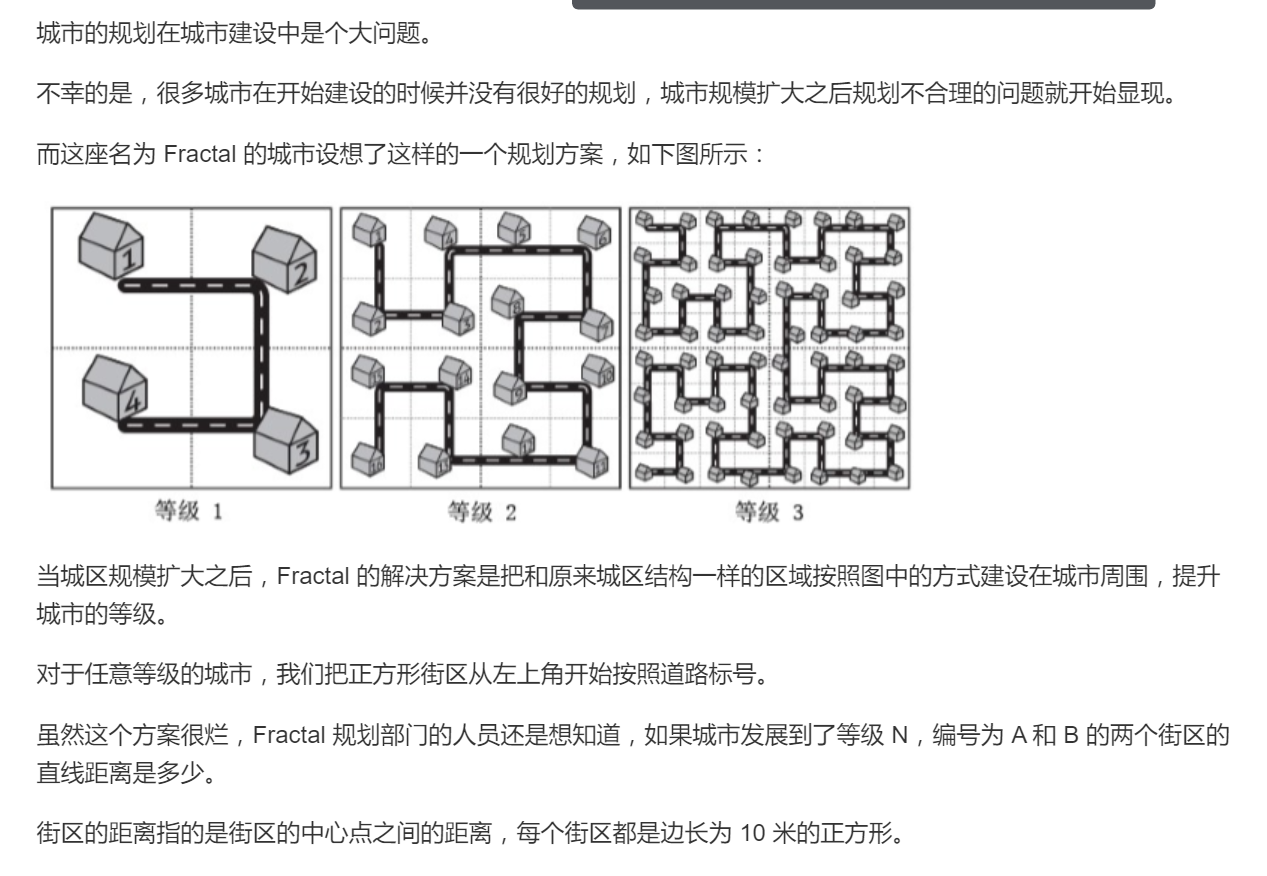
1.左上角：我们可以发现，左上角的N−1级矩阵其实就是等级为N−1，也就是上一个矩阵，顺时针旋转90°，那么既然如此的话，我们就可以综合yxc老师上课所讲的公式(补充:也就是旋转矩阵,属于大学的线性代数内容)，得出转移后的矩阵中的一点坐标从(x,y)变为(y,x)

2.左下角：同左上角，它则是逆时针旋转90°而且还要水平翻转，也即是沿着X轴对称，原本逆时针后为(y,−x)，然后要对称,x坐标不变，y坐标取反，所以坐标为(−y,−x) 也就是所谓的(2×len−1−y,len−1−x) 最难理解的坐标，具体可以画图理解

3.右上角和右下角：通过N=2级图发现，其实和N=1是一样的，并没有旋转，只是平移，则右上角坐标为(x,y+len)，右下角坐标为(x+len,y+len)
总的来说以上四种转移，都可以通过画图理解

4.还有本题数据毒瘤，四舍五入最好是double类型，而且整数类型一定要是long long，否则容易WA！

5.易错点：公式使用，double型浮点数精度问题，输出格式化问题。

样例代码

#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define PLL pair<ll,ll>
PLL calc(ll n,ll m)
{
    if (n==0)
        return make_pair(0,0);
    ll len=1LL<<(n-1),cnt=1LL<<(2*n-2);
    PLL pos=calc(n-1,m%cnt);
    ll x=pos.first,y=pos.second;
    ll z=m/cnt;
    if (z==0)
        return make_pair(y,x);
    if (z==1)
        return make_pair(x,y+len);
    if (z==2)
        return make_pair(x+len,y+len);
    return make_pair(2*len-1-y,len-1-x);
}
int main()
{
    //ios::sync_with_stdio(false);
    int t;
    cin>>t;
    while(t--)
    {
        ll n,a,b;
        cin>>n>>a>>b;
        PLL x=calc(n,a-1);
        PLL y=calc(n,b-1);
        ll dx=x.first-y.first,dy=x.second-y.second;
        double ans=(sqrt(dx*dx+dy*dy)*10);
        printf("%0.lf
",ans);
    }
    return 0;
}