101.最高的牛

原题链接：101. 最高的牛

解题思路

差分＋区间处理小操作

这道题目的一个核心要点，就是如何处理这些特殊的关系，也就是两头牛能互相看见。

其实题目中已经告诉我们如何处理，因为我们发现，题目中要求牛的身高最高，那么既然如此，我们完全可以将每一组关系(A,B),看作[A+1,B-1]这组牛身高比A,B这两头牛矮1.

各位可以画一个图，来更好理解这道题目

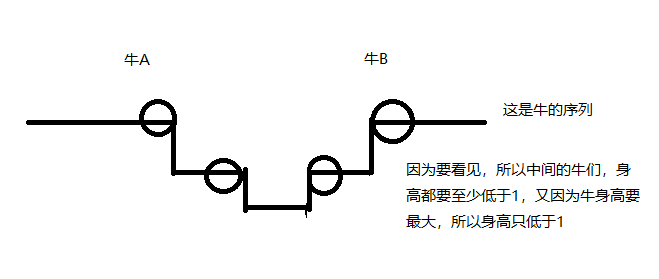
因此我们可以利用区间处理小操作，也就是前缀和加差分。设一个数组为D,D[i]为比最高牛矮多少，则D[P]=0,那么对于一组关系，我们可以这样操作，D[A+1]-,D[B]++;然后从左往右前缀和，就可以求出矮多少。具体可以看代码实现。

本题数据内部可能重复，要判重，还有[l,r]不一定l<r

样例代码

#include<bits/stdc++.h>
using namespace std;
map<pair<int,int>,bool>existed;
int c[10010],d[10010];
int main()
{
    int n,p,h,m;
    cin>>n>>p>>h>>m;
    for(int i=1;i<=m;i++)
    {
        int a,b;
        cin>>a>>b;
        if(a>b)
            swap(a,b);
        if(existed[make_pair(a,b)])
            continue;
        d[a+1]--;
        d[b]++;
        existed[make_pair(a,b)]=true;
    }
    for(int i=1;i<=n;i++)
    {
        c[i]=c[i-1]+d[i];
        cout<<h+c[i]<<endl;
    }
    return 0;
}