树状数组与线段树基础

树状数组 相对于线段树系数少很多，代码量小很多

• 快速求前缀和 or 某元素更新

• 可以解决的问题：单点修改，区间查询 or 区间修改，单点查询(差分)

• O(logn)的时间复杂度

• lowbit(x) 二进制下,x最低位1代表的值

• 编号为x的节点,统计[x - lowbit(x) + 1, x]的信息，父节点为x + lowbit(x);//奇数节点C[I]只保存a[i]

#define lowbit(i) (i & (-i))

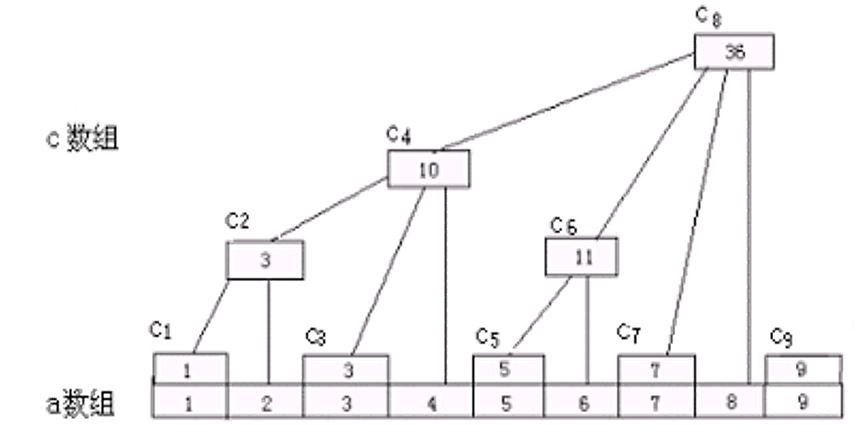
• C数组 数据输入的时候直接修改

int n,m,k,x,y,c[kN],a[kN];//a c等长 c[i](i为2,4,8...2^t)表示：1~i的和；(i为奇数)表示:a[i] 
//维护树状数组C,初始状态c,a中的元素均为0 
//i节点的值 + v，不断修改各级父节点 
void add(int i, int v){ 
    //a[i]直连c[i] 变换相同，修改c[i]的各级父节点
	for(int j = i; j <= n; j += lowbit(j)) c[j] += v;
} 
//查询区间和[1,i] 
int query(int i){
	int ans = 0;
	for(int j = i; j >= 1; j -= lowbit(j)) ans += c[j];
	return ans;
}

---

线段树 O(logn)

对数组a[n]:单点修改，单点查询，区间查询；区间修改，单点查询，区间查询；

• 单点/区间修改、询问,min,max,sum......数组a[4n]；时间复杂度均为O(logn)

• 修改： + x,*x, = x...

• 统计量、修改量可合并，通过修改量可直接修改统计量 -- 满足区级加法即可

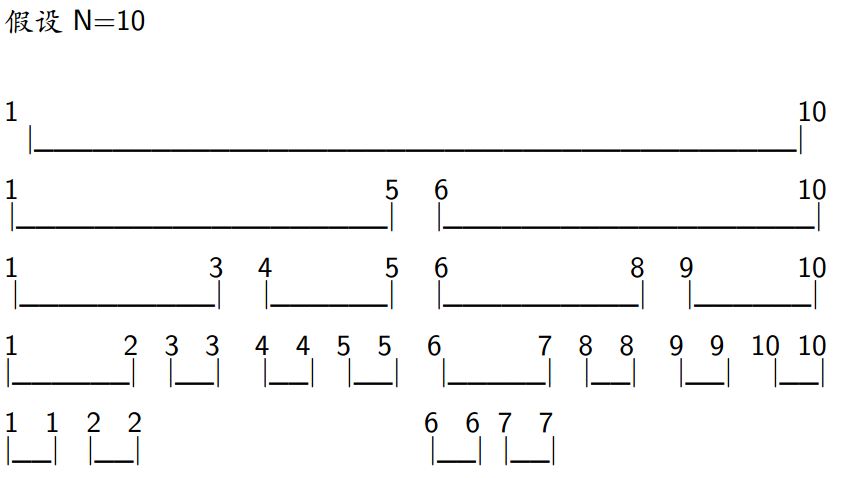
• 完全二叉树,将大区间划分为若干单位区间，单位区间为叶子结点；各节点保存一条线段;

  • 根节点区间:1~N
  • 对于树中非叶子节点[a,b],左子节点[a，(a+b)/2],右子节点[(a+b)/2 + 1, b]; ((a + b) >> 1)
  • 编号：父节点:i,左子节点:2i(i << 1),右子节点:2i + 1(i << 1 | 1)
  • lazy标签：记录当前节点变化，访问某一个节点时lazy下传;多个lazy，优先级高的先下传 ；对于某段区间中的元素进行相同的修改，若一个一个的修改效率过低。通过lazy标签，标记这一段区间的变化，在求和的时候直接通过 元素个数 * lazy值，即可表示当前区间和。
  • 预处理O(n),查询、更新O(logn)，空间换时间
  • 查找最值:根节点最值为两子树递归求出的最值中符合要求的那个
  • 区间和：总的区间和为两子树各自递归求出的区间和求和

const int kN = 1e5 + 5;
struct node{
	int sum,lazy = 0;//sum 节点代表的区间和，求最值--修改sum为minn,maxx，修改sum计算方式即可 
};
int n,m,t,x,y,k,a[kN];
node tree[4 * kN];
//i 当前节点编号,l r当前节点区间 
//递归建树 
void build_tree(int i,int l, int r){
	if(l == r){
		tree[i].sum = a[l];
		return;
	}
	int mid = l + r >> 1;
	build_tree(i << 1,l,mid);
	build_tree(i << 1 | 1,mid + 1,r);
	tree[i].sum = tree[i << 1].sum + tree[i << 1 | 1].sum;
} 
//单点修改 a[x] += y
void change1(int i, int l, int r){
	if(l == r){//到达叶子结点 
		tree[i].sum += y;
		return;
	}
	int mid = l + r >> 1;
	if(x <= mid) change1(i << 1, l, mid);
	else change1(i << 1 | 1, mid + 1, r);
	tree[i].sum = tree[i << 1].sum + tree[i << 1 | 1].sum;
}
//lazy标签下传 
void update(int i,int l, int r){
	tree[i].sum = tree[i].sum + (r - l + 1) * tree[i].lazy;
	if(l != r){
		tree[i << 1].lazy += tree[i].lazy;
		tree[i << 1 | 1].lazy += tree[i].lazy;	
	} 
	tree[i].lazy = 0;
}
//区间修改 a[x...y] + k
void change(int i, int l, int r){
	if(x <= l && y >= r){//被包含
		tree[i].lazy += k;
		return;
	}
	if(tree[i].lazy != 0) update(i,l,r);//当前节点lazy标签已使用 -- 下传 
	int mid = (l + r) >> 1;
	if(y <= mid) change(i << 1, l, mid);
	else if(x > mid) change(i << 1 | 1, mid + 1, r);
	else{
		change(i << 1, l, mid);
		change(i << 1 | 1, mid + 1, r);
	}
	tree[i].sum = tree[i << 1].sum + (mid - l + 1) * tree[i << 1].lazy + tree[i << 1 | 1].sum + (r - mid) * tree[i].lazy;
}
//区间查询 
int query(int i, int l, int r){//a[x..y]
	if(x <= l && y >= r){
		return tree[i].sum;
	}
	int ans = 0,mid = l + r >> 1;
	if(x <= mid) ans = query(i << 1, l, mid);
	if(mid < y) ans += query(i << 1 | 1, mid + 1, r);
	return ans;
}

---

线段树求最大子段和：

• 子段和存在的三种情况：在左区间；在右区间；包含左右区间分界点 -- 维护相应子段he即可