y=arctanx,则x=tany
arctanx′bai=1/tany′
tany′=(siny/cosy)′=(cosycosy-siny(-siny))/cos²y=1/cos²y
则arctanx′=cos²y=cos²y/(sin²y+cos²y)=1/(1+tan²y)=1/1+x²
故最终答案是1/(1+x²)
这一步求出了y=arctanx的导数,要求其幂级数可以观察1/(1+x²)可以展开为幂级数。故应当展开1/(1+x²)。

或者这样:

再来看刚好在收敛半径上的点:

当然可以利用高阶导数开进行泰勒展开:
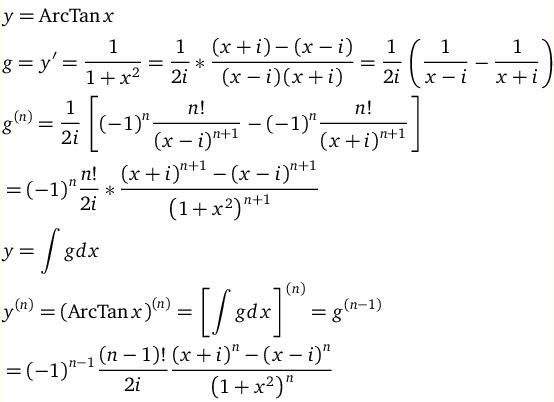
附上完整版:
1、arctanx 的麦克劳林级数展开式,必须分三段考虑:
-∞ ≤ x ≤ -1、-1 < x < +1、1 < x < +∞
2、分成zhi三段的原因是:
A、在展开过程中,必须先求导,再积分;
B、在求导跟积分之间,必须运用公比小于1的无穷等比数列求和公式;
C、运用等比求和公式时,必须考虑收敛与否,因此必须分成两部分:
|x| < 1、|x| ≥ 1;
D、在 |x| ≥ 1 时,有必须考虑积分的下限问题,因此还得再分为二。


