斐波那契数列递归次数

我们可以先实例化，从少的数列发现规律，加入我们是计算F5，则有：F5=F4+F3,F4=F3+F2,F3=F1+F2,F2=F1+F0.这时我们来计算F1,F0精确计算了多少次，为了方便计算，我们画图来表示：

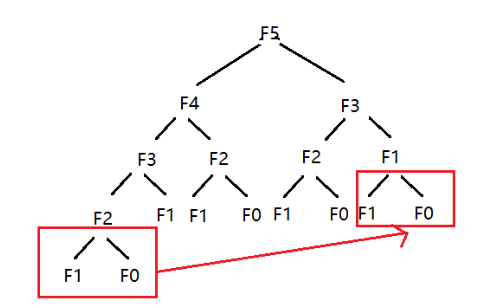
 根据二叉树结点的个数可以得出调用的次数，个数可由完全二叉树的性质得出

倒过来再换一种思路：

定义fib()如下：

int fib(int n)
    {
        count ++;
        if (n==0)
            return 1;
        else if (n==1)
            return 1;
        else
            return fib(n-1) + fib(n-2);
    }

由原来fib的地推公式得出求解次数的地推公式。

那么Count(fib(10)) = count(fib(9))  + count(fib(8)) + 1;

求解count( fib(n) ) 的次数，就是计算fib(n)递归树（是一个二叉树），叶子结点的个数。

count( fib(0) ) = 1

count( fib(1) ) = 1

count( fib(2) ) = count ( fib(1) ) + count( fib(0) )  + 1 = 3

count( fib(3) ) = count ( fib(2) ) + count( fib(1) )  + 1 = 3+1+1 = 5

这个样子计算的还是很快的

fib(10),一共调用了 177次。

其实上面是360的一道面试题

不,也是河南师范大学的考研真题，一小问，差点在程序里再模拟一下fib让程序自己算去了(也能出结果但是格式上看着好难受)，但是这样又明显违背了主程序和被调用函数的分离，只有自己记住结论再用一个简单的printf函数打印出来才是最合适的答卷方式