Description
A young schoolboy would like to calculate the sum
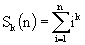
for some fixed natural k and different natural n. He observed that calculating ik for all i (1<=i<=n) and summing up results is a too slow way to do it, because the number of required arithmetical operations increases as n increases. Fortunately, there is another method which takes only a constant number of operations regardless of n. It is possible to show that the sum Sk(n) is equal to some polynomial of degree k+1 in the variable n with rational coefficients, i.e.,
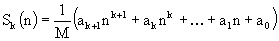
We require that integer M be positive and as small as possible. Under this condition the entire set of such numbers (i.e. M, ak+1, ak, ... , a1, a0) will be unique for the given k. You have to write a program to find such set of coefficients to help the schoolboy make his calculations quicker.
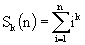
for some fixed natural k and different natural n. He observed that calculating ik for all i (1<=i<=n) and summing up results is a too slow way to do it, because the number of required arithmetical operations increases as n increases. Fortunately, there is another method which takes only a constant number of operations regardless of n. It is possible to show that the sum Sk(n) is equal to some polynomial of degree k+1 in the variable n with rational coefficients, i.e.,
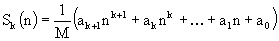
We require that integer M be positive and as small as possible. Under this condition the entire set of such numbers (i.e. M, ak+1, ak, ... , a1, a0) will be unique for the given k. You have to write a program to find such set of coefficients to help the schoolboy make his calculations quicker.
Input
The input file contains a single integer k (1<=k<=20).
Output
Write integer numbers M, ak+1, ak, ... , a1, a0
to the output file in the given order. Numbers should be separated by
one space. Remember that you should write the answer with the smallest
positive M possible.
Sample Input
2
Sample Output
6 2 3 1 0
Source
【分析】
题意就是给出一个k,找一个最小的M使得 中a[i]皆为整数.
中a[i]皆为整数.
这个涉及到伯努利数的一些公式,如果不知道的话基本没法做..
1. 伯努利数与自然数幂的关系:
2. 伯努利数递推式:

1 /* 2 宋代朱敦儒 3 《西江月·世事短如春梦》 4 世事短如春梦,人情薄似秋云。不须计较苦劳心。万事原来有命。 5 幸遇三杯酒好,况逢一朵花新。片时欢笑且相亲。明日阴晴未定。 6 */ 7 #include <cstdio> 8 #include <cstring> 9 #include <algorithm> 10 #include <cmath> 11 #include <queue> 12 #include <vector> 13 #include <iostream> 14 #include <string> 15 #include <ctime> 16 #define LOCAL 17 const int MAXN = 20 + 10; 18 const double Pi = acos(-1.0); 19 using namespace std; 20 typedef long long ll; 21 ll gcd(ll a, ll b){return b == 0? a: gcd(b, a % b);} 22 struct Num{ 23 ll a, b;//分数,b为分母 24 Num(ll x = 0, ll y = 0) {a = x;b = y;} 25 void update(){ 26 ll tmp = gcd(a, b); 27 a /= tmp; 28 b /= tmp; 29 } 30 Num operator + (const Num &c){ 31 ll fz = a * c.b + b * c.a, fm = b * c.b; 32 if (fz == 0) return Num(0, 1); 33 ll tmp = gcd(fz, fm); 34 return Num(fz / tmp, fm / tmp); 35 } 36 }B[MAXN], A[MAXN]; 37 ll C[MAXN][MAXN]; 38 39 void init(){ 40 //预处理组合数 41 for (int i = 0; i < MAXN; i++) C[i][0] = C[i][i] = 1; 42 for (int i = 2; i < MAXN; i++) 43 for (int j = 1; j < MAXN; j++) C[i][j] = C[i - 1][j] + C[i - 1][j - 1]; 44 //预处理伯努利数 45 B[0] = Num(1, 1); 46 for (int i = 1; i < MAXN; i++){ 47 Num tmp = Num(0, 1), add; 48 for (int j = 0; j < i; j++){ 49 add = B[j]; 50 add.a *= C[i + 1][j]; 51 tmp = tmp + add; 52 } 53 if (tmp.a) tmp.b *= -(i + 1); 54 tmp.update(); 55 B[i] = tmp; 56 } 57 } 58 void work(){ 59 int n; 60 scanf("%d", &n); 61 ll M = n + 1, flag = 0, Lcm; 62 A[0] = Num(0, 1); 63 for (int i = 1; i <= n + 1; i++){ 64 if (B[n + 1 - i].a == 0) {A[i] = Num(0, 1);continue;} 65 Num tmp = B[n + 1 - i]; 66 tmp.a *= C[n + 1][i];//C[n+1][i] = C[n + 1][n + 1 - i] 67 tmp.update(); 68 if (flag == 0) Lcm = flag = tmp.b; 69 A[i] = tmp; 70 } 71 A[n] = A[n] + Num(n + 1, 1); 72 73 for (int i = 2; i <= n + 1; i++){ 74 if (A[i].a == 0) continue; 75 Lcm = (Lcm * A[i].b) / gcd(Lcm, A[i].b); 76 } 77 if (Lcm < 0) Lcm *= -1; 78 M *= Lcm; 79 printf("%lld", M); 80 for (int i = n + 1; i >= 0; i--) printf(" %lld", A[i].a * Lcm / A[i].b); 81 } 82 83 int main(){ 84 85 init(); 86 work(); 87 //printf("%lld ", C[5][3]); 88 return 0; 89 }

