题目
每天 BBS 都要从家里经过城市中的一段路到学校刷五三。城市中一共有 n 个路口
和 m 条双向道路,每条双向道路都连接着两个路口 a i 、b i 且有一定的时间花费 v i 。BBS
家编号为 1,学校编号为 n。今天,BBS 由于个人卫生综合征导致他很迟才离开家,他
想用膜法改变 k 条道路的长度使通过其的时间花费 v i 变为 0。现在他问你改变道路长度
之后他到学校的最小时间花费是多少?
输入格式:
第一行为三个整数 n、m、k,接下来的 m 行每行三个整数 a i ,b i ,v i ,分别表示这条路连
着的两个路口和通过其所用的时间。
输出格式:
一个整数,表示 BBS 到学校的最小时间花费。
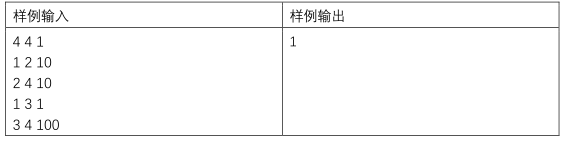
样例解释:
更新 3->4 的道路,最短路线为 1->3->4,用时为 1+0=1。
数据范围:
对于 100%的数据:1<=n<=10000,1<=m<=50000,1<=k<=20,1<=v i <=1000000。
题解
题意还是比较易懂的。给定一个无向图,可以把k条路的长度变为0,求1到n的最短路。
这题似乎没有部分分……那就讲正解吧。
插播:话说这题是有原题的:(BZOJ2763)[JLOI2011]飞行路线。
这题的正解是分层图最短路。
建立一个有k+1个层的图,每次将花费变为0,层数+1,初始0层,最多k层,所以最多减少k条路。(当然,一条路减少多次是没有意义的)
在实际应用时,由于图是一样的,只需要分别记录这k层中每层n个点到1号点的最短路(代码中的d数组)和访问情况(代码中的vis数组)即可。
还有,一定要用dijkstra!一定要用dijkstra!一定要用dijkstra!用spfa会T!(某巨神就中招了……)
代码

1 #include <stdio.h> 2 #include <string.h> 3 #include <queue> 4 #define N 10005 5 #define K 22 6 using namespace std; 7 int n,m,k,d[N][K];char vis[N][K]; 8 int ne=0,h[N];struct edge{int to,w,x;}e[100010]; 9 inline void ins(int s,int t,int w) { 10 e[++ne].to=t;e[ne].w=w;e[ne].x=h[s];h[s]=ne; 11 } 12 struct node { 13 int a,l,dis; 14 bool operator<(const node &b)const { 15 return dis>b.dis; 16 } 17 }; 18 priority_queue<node> q; 19 inline void tt(int a,int l,int p) { 20 if(!vis[a][l]&&d[a][l]>p) { 21 d[a][l]=p; 22 q.push({a,l,p}); 23 } 24 } 25 void dijkstra() { 26 node u;edge v; 27 memset(d,66,sizeof(d)); 28 d[1][0]=0; 29 q.push({1,0,0}); 30 while(!q.empty()) { 31 u=q.top();q.pop(); 32 vis[u.a][u.l]=1; 33 for(int i=h[u.a];i;i=v.x) { 34 v=e[i]; 35 tt(v.to,u.l,u.dis+v.w); 36 if(u.l<k) tt(v.to,u.l+1,u.dis); 37 } 38 } 39 } 40 int main() { 41 int a,b,c; 42 scanf("%d%d%d",&n,&m,&k); 43 for(int i=0;i<m;++i) { 44 scanf("%d%d%d",&a,&b,&c); 45 ins(a,b,c);ins(b,a,c); 46 } 47 dijkstra(); 48 a=d[n][0]; 49 for(int i=1;i<=k;++i) if(d[n][i]<a) a=d[n][i]; 50 printf("%d",a); 51 return 0; 52 }
