Codeforces Round #340 (Div. 2) D

D. Polyline

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

There are three points marked on the coordinate plane. The goal is to make a simple polyline, without self-intersections and self-touches, such that it passes through all these points. Also, the polyline must consist of only segments parallel to the coordinate axes. You are to find the minimum number of segments this polyline may consist of.

Input

Each of the three lines of the input contains two integers. The i-th line contains integers x_i and y_i ( - 10⁹ ≤ x_i, y_i ≤ 10⁹) — the coordinates of the i-th point. It is guaranteed that all points are distinct.

Output

Print a single number — the minimum possible number of segments of the polyline.

Sample test(s)

Input

1 -1
1 1
1 2

Output

1

Input

-1 -1
-1 3
4 3

Output

2

Input

1 1
2 3
3 2

Output

3

Note

The variant of the polyline in the first sample:

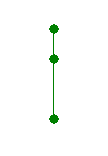
The variant of the polyline in the second sample:

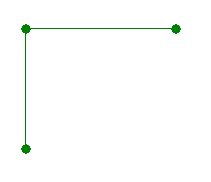
The variant of the polyline in the third sample:

          

题意 三个点 划平行于坐标轴的线 没有自生相交

问有多少个线段组成 

特别样例

0 0

0 1

1 2

这把  hack 了别人几发   代码写搓了 现在补  

#include<iostream>
#include<cstdio>
using namespace std;
__int64 x1,y1,x2,y2,x3,y3;
int main()
{
    scanf("%I64d %I64d %I64d %I64d %I64d %I64d",&x1,&y1,&x2,&y2,&x3,&y3);
    if((x1==x2&&x2==x3)||(y1==y2&&y2==y3))
        printf("1
");
    else
    {
        if((x2==x3&&y3>y2&&(y1>=y3||y1<=y2))||(x2==x3&&y2>y3&&(y1>=y2||y1<=y3))||

(x1==x2&&y1>y2&&(y3>=y1||y3<=y2))||(x1==x2&&y1<y2&&(y3>=y2||y3<=y1))||(x1==x3&&y1>y3&&(y2>=y1||y2<=y3))||(x1==x3&&y1<y3&&(y2>=y3||y2<=y1))||

(y1==y2&&x1<x2&&(x3<=x1||x3>=x2))||(y1==y2&&x1>x2&&(x3>=x1||x3<=x2))||(y2==y3&&x3>x2&&(x1>=x3||x1<=x2))||(y2==y3&&x2>x3&&(x1>=x2||x1<=x3))||

(y1==y3&&x1<x3&&(x2<=x1||x2>=x3))||(y1==y3&&x1>x3&&(x2>=x1||x2<=x3)))
            printf("2
");
        else
            printf("3
");
    }
    return 0;
}