HDU 5692 线段树+dfs序

Snacks

Time Limit: 10000/5000 MS (Java/Others)    Memory Limit: 65536/65536 K (Java/Others)
Total Submission(s): 1779    Accepted Submission(s): 427

Problem Description

百度科技园内有n 个零食机，零食机之间通过n−1 条路相互连通。每个零食机都有一个值v ，表示为小度熊提供零食的价值。

由于零食被频繁的消耗和补充，零食机的价值v 会时常发生变化。小度熊只能从编号为0的零食机出发，并且每个零食机至多经过一次。另外，小度熊会对某个零食机的零食有所偏爱，要求路线上必须有那个零食机。

为小度熊规划一个路线，使得路线上的价值总和最大。

 

Input

输入数据第一行是一个整数T(T≤10) ，表示有T 组测试数据。

对于每组数据，包含两个整数n,m(1≤n,m≤100000) ，表示有n 个零食机，m 次操作。

接下来n−1 行，每行两个整数x 和y(0≤x,y<n) ，表示编号为x 的零食机与编号为y 的零食机相连。

接下来一行由n 个数组成，表示从编号为0到编号为n−1 的零食机的初始价值v(|v|<100000) 。

接下来m 行，有两种操作：0 x y ，表示编号为x 的零食机的价值变为y ；1 x ，表示询问从编号为0的零食机出发，必须经过编号为x 零食机的路线中，价值总和的最大值。

本题可能栈溢出，辛苦同学们提交语言选择c++，并在代码的第一行加上：

`#pragma comment(linker, "/STACK:1024000000,1024000000") `

 

Output

对于每组数据，首先输出一行”Case #?:”，在问号处应填入当前数据的组数，组数从1开始计算。

对于每次询问，输出从编号为0的零食机出发，必须经过编号为x 零食机的路线中，价值总和的最大值。

 

Sample Input

1

6 5

0 1

1 2

0 3

3 4

5 3

7 -5 100 20 -5 -7

1 1

1 3

0 2 -1

1 1

1 5

 

Sample Output

Case #1:

102

27

2

20

 

Source

2016"百度之星" - 初赛（Astar Round2A）

 

题意：中文题面

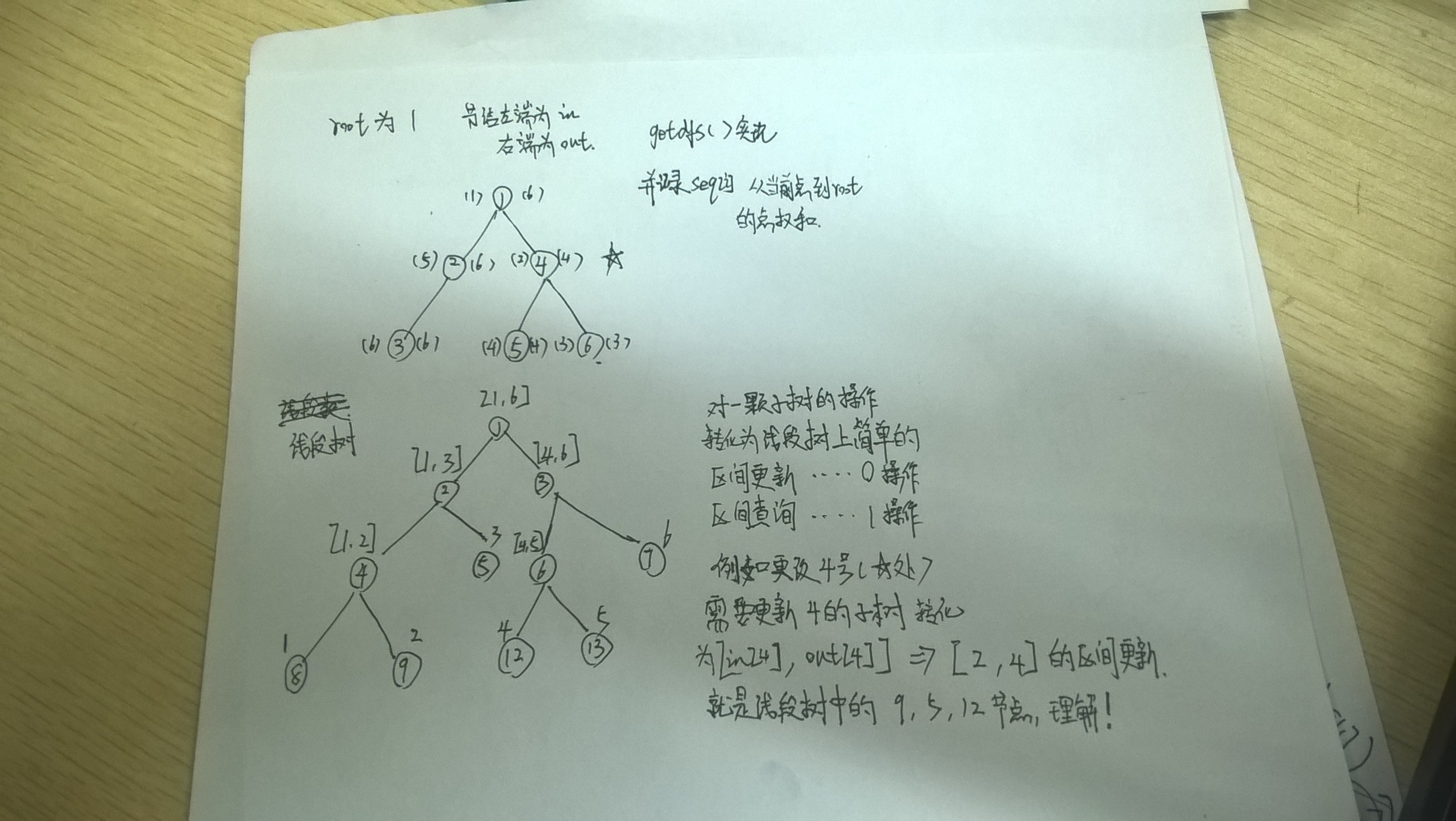
题解：第一次写线段树+dfs序列

 

/******************************
code by drizzle
blog: www.cnblogs.com/hsd-/
^ ^    ^ ^
 O      O
******************************/
#include<bits/stdc++.h>
#include<map>
#include<set>
#include<cmath>
#include<queue>
#include<bitset>
#include<math.h>
#include<vector>
#include<string>
#include<stdio.h>
#include<cstring>
#include<iostream>
#include<algorithm>
#pragma comment(linker, "/STACK:102400000,102400000")
using namespace std;
#define  A first
#define B second
const int mod=1000000007;
const int MOD1=1000000007;
const int MOD2=1000000009;
const double EPS=0.00000001;
//typedef long long ll;
typedef __int64 ll;
const ll MOD=1000000007;
const int INF=1000000010;
const ll MAX=1ll<<55;
const double eps=1e-5;
const double inf=~0u>>1;
const double pi=acos(-1.0);
typedef double db;
typedef unsigned int uint;
typedef unsigned long long ull;
int T,n,m,x,judge,nedge=0,dfn, y;
struct node
{
    int ed;
    int pre;
} N[200005];
int pre[200005],in[200005],out[200005];
ll v[200005];
ll seq[200005];
ll fuck;
struct tree
{
    int l,r;
    ll lazy;
    ll maxn;
} tree[400005];
inline void add(int st,int ed)
{
    nedge++;
    N[nedge].ed=ed;
    N[nedge].pre=pre[st];
    pre[st]=nedge;
}
inline void getdfs(int x,int y,ll s)
{
    s+=v[x];
    in[x]=++dfn;
    seq[dfn]=s;
    for(int i=pre[x]; i; i=N[i].pre)
    {
        if(N[i].ed!=y)
        {
            getdfs(N[i].ed,x,s);
        }
    }
    out[x]=dfn;
}
inline void pushdown(int root)
{
    if(tree[root].lazy==0) return;
    tree[root<<1].lazy+=tree[root].lazy;
    tree[root<<1|1].lazy+=tree[root].lazy;
    tree[root<<1].maxn+=tree[root].lazy;
    tree[root<<1|1].maxn+=tree[root].lazy;
    tree[root].lazy=0;
}
inline void buildtree(int root,int left,int right)
{
    tree[root].l=left;
    tree[root].r=right;
    tree[root].lazy=0;
    if(left==right)
    {
        tree[root].maxn=seq[left];
        return ;
    }
    int mid=(left+right)>>1;
    buildtree(root<<1,left,mid);
    buildtree(root<<1|1,mid+1,right);
    tree[root].maxn=max(tree[root<<1].maxn,tree[root<<1|1].maxn);
}
inline void updata(int root,int in,int out,ll after)
{
    if(in==tree[root].l&&tree[root].r==out)
    {
        tree[root].lazy+=after;
        tree[root].maxn+=after;
        return ;
    }
    pushdown(root);
    int mid=(tree[root].l+tree[root].r)>>1;
    if(out<=mid)
        updata(root<<1,in,out,after);
    else
    {
        if(in>mid)
            updata(root<<1|1,in,out,after);
        else
        {
            updata(root<<1,in,mid,after);
            updata(root<<1|1,mid+1,out,after);
        }
    }
    tree[root].maxn=max(tree[root<<1].maxn,tree[root<<1|1].maxn);
}
inline ll query(int root,int in,int out)
{
    if(in==tree[root].l&&tree[root].r==out)
    {
        return tree[root].maxn;
    }
    pushdown(root);
    int mid=(tree[root].l+tree[root].r)>>1;
    if(out<=mid)
        return query(root<<1,in,out);
    else
    {
        if(in>mid)
            return query(root<<1|1,in,out);
        else
            return max(query(root<<1,in,mid),query(root<<1|1,mid+1,out));
    }
}
void init()
{
    memset(tree,0,sizeof(tree));
    memset(N,0,sizeof(N));
    memset(pre,0,sizeof(pre));
    memset(in,0,sizeof(in));
    memset(out,0,sizeof(out));
    memset(v,0,sizeof(v));
    memset(seq,0,sizeof(seq));
    nedge=0;
    dfn=0;
}
int main()
{
        scanf("%d",&T);
        for(int i=1; i<=T; i++)
        {
            init();
            scanf("%d %d",&n,&m);
            for(int j=1; j<n; j++)
            {
                scanf("%d %d",&x,&y);
                x++;
                y++;
                add(x,y);
                add(y,x);
            }
            for(int j=1; j<=n; j++)
                scanf("%I64d",&v[j]);
            getdfs(1,1,0);
            buildtree(1,1,n);
            printf("Case #%d:
",i);
            for(int j=1; j<=m; j++)
            {
                scanf("%d %d",&judge,&x);
                if(judge==0)
                {
                    scanf("%I64d",&fuck);
                    x++;
                    ll exm=fuck;
                    fuck=fuck-v[x];
                    updata(1,in[x],out[x],fuck);
                    v[x]=exm;
                }
                else
                {
                    x++;
                    printf("%I64d
",query(1,in[x],out[x]));
                }
            }
        }
    return 0;
}