"Night gathers, and now my watch begins. It shall not end until my death. I shall take no wife, hold no lands, father no children. I shall wear no crowns and win no glory. I shall live and die at my post. I am the sword in the darkness. I am the watcher on the walls. I am the shield that guards the realms of men. I pledge my life and honor to the Night's Watch, for this night and all the nights to come." — The Night's Watch oath.
With that begins the watch of Jon Snow. He is assigned the task to support the stewards.
This time he has n stewards with him whom he has to provide support. Each steward has his own strength. Jon Snow likes to support a steward only if there exists at least one steward who has strength strictly less than him and at least one steward who has strength strictly greater than him.
Can you find how many stewards will Jon support?
First line consists of a single integer n (1 ≤ n ≤ 105) — the number of stewards with Jon Snow.
Second line consists of n space separated integers a1, a2, ..., an (0 ≤ ai ≤ 109) representing the values assigned to the stewards.
Output a single integer representing the number of stewards which Jon will feed.
2
1 5
0
3
1 2 5
1
In the first sample, Jon Snow cannot support steward with strength 1 because there is no steward with strength less than 1 and he cannot support steward with strength 5 because there is no steward with strength greater than 5.
In the second sample, Jon Snow can support steward with strength 2 because there are stewards with strength less than 2 and greater than 2.
题意：给你n个数 输出去掉最小值最大值的之后的数列的个数
题解：水
1 #include <iostream> 2 #include <cstdio> 3 #include <cstdlib> 4 #include <cstring> 5 #include <algorithm> 6 #include <stack> 7 #include <queue> 8 #include <cmath> 9 #include <map> 10 #define ll __int64 11 #define mod 1000000007 12 #define dazhi 2147483647 13 using namespace std; 14 int n; 15 int a[100005]; 16 int main() 17 { 18 scanf("%d",&n); 19 int minx=1000000001; 20 int maxn=0; 21 for(int i=1;i<=n;i++) 22 { 23 scanf("%d",&a[i]); 24 minx=min(minx,a[i]); 25 maxn=max(maxn,a[i]); 26 } 27 int ans=0; 28 if(minx==maxn){ 29 printf("0 "); 30 return 0; 31 } 32 else 33 { 34 for(int i=1;i<=n;i++) 35 { 36 if(a[i]==minx) 37 ans++; 38 if(a[i]==maxn) 39 ans++; 40 } 41 } 42 printf("%d ",n-ans); 43 return 0; 44 }
Jon fought bravely to rescue the wildlings who were attacked by the white-walkers at Hardhome. On his arrival, Sam tells him that he wants to go to Oldtown to train at the Citadel to become a maester, so he can return and take the deceased Aemon's place as maester of Castle Black. Jon agrees to Sam's proposal and Sam sets off his journey to the Citadel. However becoming a trainee at the Citadel is not a cakewalk and hence the maesters at the Citadel gave Sam a problem to test his eligibility.
Initially Sam has a list with a single element n. Then he has to perform certain operations on this list. In each operation Sam must remove any element x, such that x > 1, from the list and insert at the same position 
, 
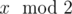, sequentially. He must continue with these operations until all the elements in the list are either 0 or 1.
Now the masters want the total number of 1s in the range l to r (1-indexed). Sam wants to become a maester but unfortunately he cannot solve this problem. Can you help Sam to pass the eligibility test?
The first line contains three integers n, l, r (0 ≤ n < 250, 0 ≤ r - l ≤ 105, r ≥ 1, l ≥ 1) – initial element and the range l to r.
It is guaranteed that r is not greater than the length of the final list.
Output the total number of 1s in the range l to r in the final sequence.
7 2 5
4
10 3 10
5
Consider first example:
Elements on positions from 2-nd to 5-th in list is [1, 1, 1, 1]. The number of ones is 4.
For the second example:
Elements on positions from 3-rd to 10-th in list is [1, 1, 1, 0, 1, 0, 1, 0]. The number of ones is 5.
题意：给你一个数x 分成{x/2,x%2,x/2} 直到每一项为0或1 问你[l,r]内1的个数。
题解：对一个三叉树dfs dp[x]表示 x分解之后的数列的长度
1 #include <iostream> 2 #include <cstdio> 3 #include <cstdlib> 4 #include <cstring> 5 #include <algorithm> 6 #include <stack> 7 #include <queue> 8 #include <cmath> 9 #include <map> 10 #define ll __int64 11 #define mod 1000000007 12 #define dazhi 2147483647 13 using namespace std; 14 ll n,l,r; 15 map<ll,ll> dp; 16 ll dfs(ll x) 17 { 18 if(x!=0) 19 dp[x]+=2*dfs(x/2)+1; 20 return dp[x]; 21 } 22 int main() 23 { 24 dp[1]=1; 25 scanf("%I64d %I64d %I64d",&n,&l,&r); 26 dp.clear(); 27 ll m=n; 28 dfs(m); 29 ll re=0; 30 for(ll i=l; i<=r; i++) 31 { 32 ll exm=n; 33 ll ans=0; 34 while(exm) 35 { 36 if(ans+dp[exm/2]+1==i) 37 { 38 if(exm%2==1) 39 re++; 40 break; 41 } 42 else 43 { 44 if(ans+dp[exm/2]>i) 45 exm/=2; 46 else 47 { 48 if(ans+dp[exm/2]==i) 49 { 50 re++; 51 break; 52 } 53 ans+=dp[exm/2]+1; 54 } 55 } 56 if(ans==i) 57 { 58 re++; 59 break; 60 } 61 } 62 } 63 printf("%I64d ",re); 64 return 0; 65 }