Problem Description
医学界发现的新病毒因其蔓延速度和Internet上传播的"红色病毒"不相上下,被称为"红色病毒",经研究发现,该病毒及其变种的DNA的一条单链中,胞嘧啶,腺嘧啶均是成对出现的。
现在有一长度为N的字符串,满足一下条件:
(1) 字符串仅由A,B,C,D四个字母组成;
(2) A出现偶数次(也可以不出现);
(3) C出现偶数次(也可以不出现);
计算满足条件的字符串个数.
当N=2时,所有满足条件的字符串有如下6个:BB,BD,DB,DD,AA,CC.
由于这个数据肯能非常庞大,你只要给出最后两位数字即可.
现在有一长度为N的字符串,满足一下条件:
(1) 字符串仅由A,B,C,D四个字母组成;
(2) A出现偶数次(也可以不出现);
(3) C出现偶数次(也可以不出现);
计算满足条件的字符串个数.
当N=2时,所有满足条件的字符串有如下6个:BB,BD,DB,DD,AA,CC.
由于这个数据肯能非常庞大,你只要给出最后两位数字即可.
Input
每组输入的第一行是一个整数T,表示测试实例的个数,下面是T行数据,每行一个整数N(1<=N<2^64),当T=0时结束.
Output
对于每个测试实例,输出字符串个数的最后两位,每组输出后跟一个空行.
Sample Input
4
1
4
20
11
3
14
24
6
0
Sample Output
Case 1: 2
Case 2: 72
Case 3: 32
Case 4: 0
Case 1: 56
Case 2: 72
Case 3: 56
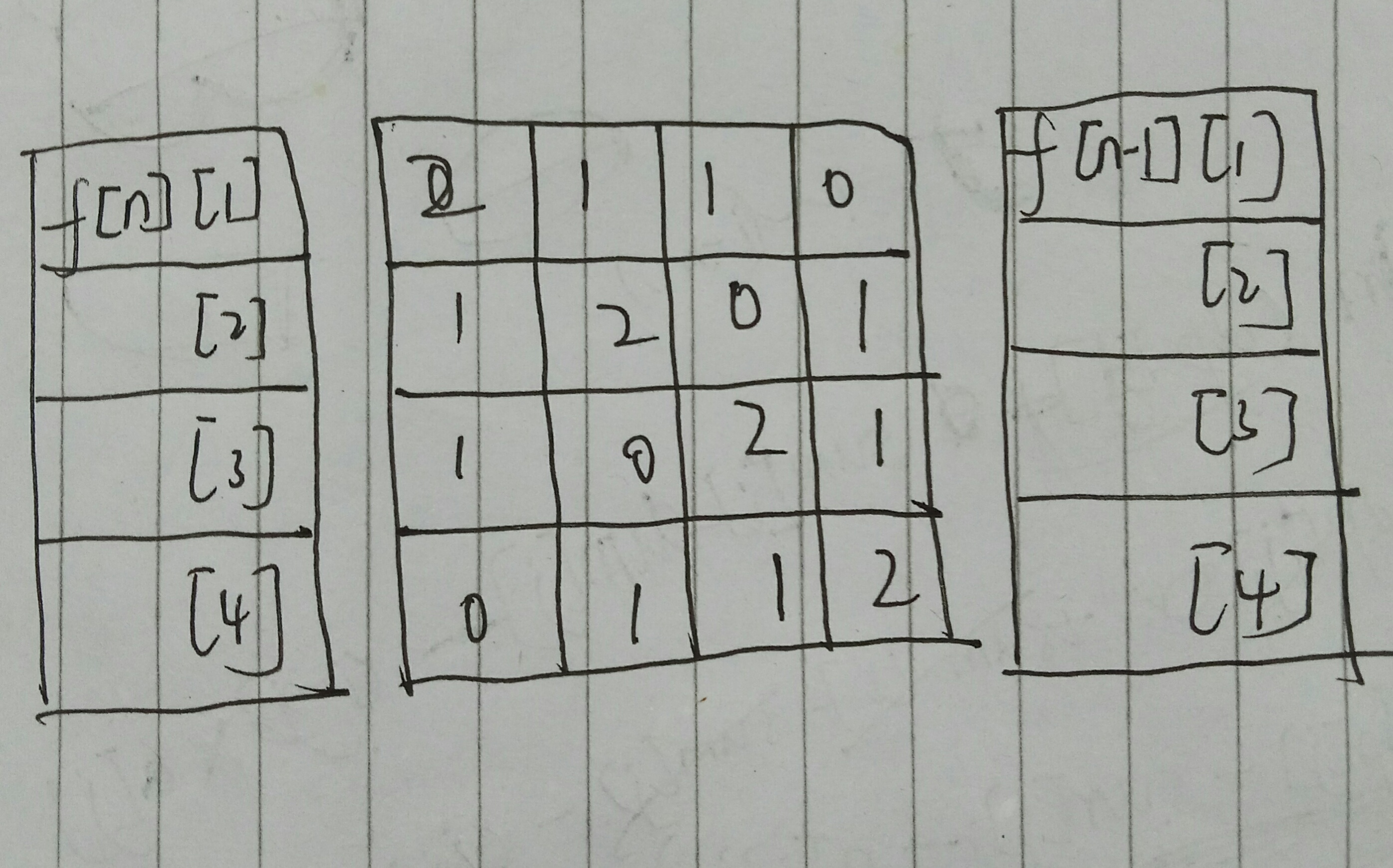
矩阵思路:用f[i][1]表示前i个里面有偶数个A和偶数个C,f[i][2]表示....然后易得。
#include<cstdio> #include<cstdlib> #include<cstring> #include<iostream> #include<algorithm> using namespace std; #define LL long long const int maxn=5; const int Mod=100; struct mat { int m[maxn][maxn]; mat(){memset(m,0,sizeof(m));}; mat friend operator *(mat a,mat b) { mat d; for(int i=1;i<=4;i++) for(int j=1;j<=4;j++) for(int k=1;k<=4;k++) d.m[i][j]=(d.m[i][j]+a.m[i][k]*b.m[k][j])%Mod; return d; } mat friend operator ^(mat a,LL n) { mat d; for(int i=1;i<=4;i++) d.m[i][i]=1; while(n){ if(n&1) d=d*a; a=a*a; n>>=1; } return d; } }; int main() { int i,Case,T; LL n; while(~scanf("%d",&T)&&T){ Case=0; while(T--){ scanf("%lld",&n); mat b,ans; b.m[1][1]=2;b.m[1][2]=1;b.m[1][3]=1; b.m[2][2]=2;b.m[2][1]=1;b.m[2][4]=1; b.m[3][3]=2;b.m[3][1]=1;b.m[3][4]=1; b.m[4][4]=2;b.m[4][2]=1;b.m[4][3]=1; ans=b^n; printf("Case %d: %d ",++Case,ans.m[1][1]); } printf(" "); } return 0; }
然而不小心看到其他方法,一下子蒙圈了,QwQ:
方法1,找循环结构,不难想。
方法2,DP,还没有看,多半和循环结构有关。
方法3,指数形母函数,和泰勒公式有关。
高数学了泰勒,我之前也学了母函数,不过比较基础:nmphy的母函数。
然后就翻论文看各种母函数。
后面发现母函数还可以解决【树的计数】问题,因为之前看过Prufer和Cayley 算法,然后就去看母函数来解决树的计数。
外文的看不懂,GG。
中文里感觉好的:
http://www.docin.com/p-538824587.html kb就是kb,大佬!
http://www.docin.com/p-140832665.html 这篇论文和其他论文有相似之处,也有独到之处,还不错。
反正越看越觉得自己数学不够用。
http://ishare.iask.sina.com.cn/f/67448295.html 史老爷,看过他的数学分析的举个手。
学会了高阶母函数再来补充!
2017-11-15
--------------------------------------------------------------分界线就是我----------------------------------------------------------------------
2017-11-20:
感觉母函数很神奇,很强大,用处太多了。
ORZ!!!
#include<cstdio> #include<cstdlib> #include<cstring> #include<iostream> #include<algorithm> using namespace std; #define LL long long int pow(int a,LL n) { int ans=1; while(n){ if(n&1) ans*=a; ans%=100; a=a*a%100; n>>=1; } return ans; } int main() { int T,i,j,ans,Case,m; LL n; while(~scanf("%d",&T)){ if(T==0) return 0; Case=0; for(i=1;i<=T;i++){ scanf("%lld",&n); printf("Case %d: ",++Case); printf("%d ",(pow(4,n-1)+pow(2,n-1))%100); } printf(" "); } return 0; }

反正就是用这样【简单的公式】就能推出来,所以有时间的伙伴一定要看看母函数。
这里不做解释,自己看书,毕竟我也讲不清楚。
