【堆（是时候该入土了）】

简介

　　堆(Heap)是计算机科学中一类特殊的数据结构的统称。堆通常是一个可以被看做一棵完全二叉树的数组对象。

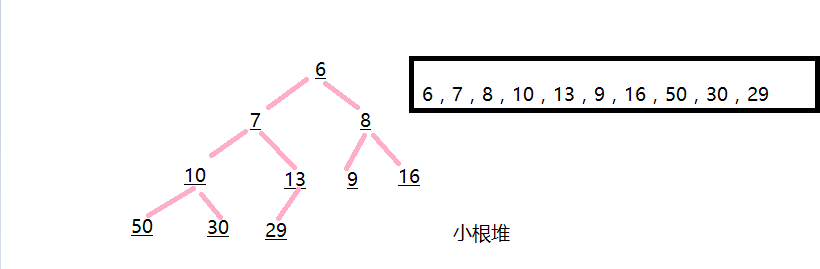
　　它符合一种规律，如果每个根结点的值比它所有的子节点的值要大，就叫大根堆，反之叫做小根堆

建堆

 首先你得有一个数组，然后我们一步步让它符合堆的规则（以下为大根堆）

首先找到最后一个非叶子结点（因为叶子结点没有子节点），然后一步一步回到根结点，保证这个堆里的每一个根结点都小于它的子节点

for(int i=size/2-1;i>=0;--i)
    make(a,i,size);

然后开始让它们符合规律

void make(int now, int size)
{
        int left=2*now+1;//左儿子 
        int right=2*now+2;//右儿子 
        int max=now;//假设他是最大的 
        //把它与孩子节点作比较，如果孩子节点大于它，
        //为了保持堆规律，我们要让现在这个节点最大 
        if(left<size&&a[left]>a[max])
            max=left;
        if(right<size&&a[right]>a[max])
            max=right;
            
        if(max!=now)
        {
            swap(a[max],a[now]);
            make(max,size);//继续向下递归，因为交换后孩子节点就小了，可能不符合堆规律 
        }
}

然后一个最大堆就建好了

堆排序

现在有了一个大根堆了，但是要排序，怎么排呢？首先，这个大根堆的顶部，一定是这些数中最大的，我们只需要把这个最大的取出来，然后再来维护大根堆，再取出最大的.......

#include <bits/stdc++.h>
using namespace std;
int a[100005],n;
void make(int now,int size)
{
    int left=2*now+1;
    int right=2*now+2;
    int max=now;
    if(left<size&&a[left]>a[max])
        max=left;
    if(right<size&&a[right]>a[max])
        max=right;
    if(max!=now)
    {
        swap(a[max],a[now]);
        make(max,size);
    }
}

void heap_sort(int n)
{
    for(int i=n/2-1;i>=0;--i)
           make(i,n);
    for(int i=n-1;i>=0;i--)
    {
        swap(a[0], a[i]);
        cout<<a[i]<<" ";        
        make(0,i);       
    }
}
 
int main()
{
    cin>>n;
    for(int i=0;i<n;i++)
    {
           scanf("%d",&a[i]);
    }
    heap_sort(n);
    return 0;
}

小根堆排序改一下符号即可