堆排序算法

　　在了解堆排序算法的原理之前，我们必须先来了解一下什么是堆？堆就是一个近似的完全的二叉树。那什么又是完全二叉树呢？完全二叉树的定义如下：

　　若设二叉树的高度为h，除第 h 层外，其它各层 (1～h-1) 的结点数都达到最大个数，第 h 层从右向左连续缺若干结点，这就是完全二叉树。完全二叉树的图示如下：

　　

　　由上面这幅图可看出完全二叉树的特点：最后一层从左向右连续缺失节点。

　　堆就是将数组表示为完全二叉树的形式，那么如何把数组转换成堆呢？接下来以一个图演示数组转换成堆。假设有一个整型数组：｛5，4，8，3，2，1｝

  了解完堆的概念之后，我们还需要知道大根堆：大根堆中就是每个父节点的数据大于子节点中的数据。小根堆则相反，每个父节点的数据小于子节点。下面就是一个大根堆跟一个小根堆

                           大根堆                                                                                        小根堆

   堆排序的原理就是每次将未排序数组构建成一个大根堆或者是一个小根堆，得到根节点便是未排序数组中的最大或者是最小值，然后将根节点即数组中第一个数据跟未排序数组中的最后一个元素即进行交换。然后将未排序数组的数量减一，再次构建大根堆或者小根堆。以此类推，直到未排序数组剩下一个元素。下面以大根堆为例：

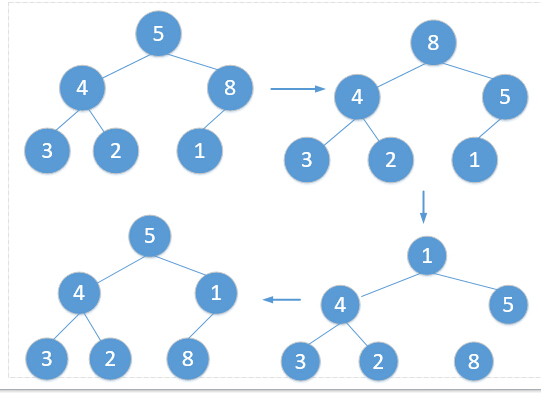
   按照上图的做法不断循环直到最后未排序数组中剩下一个元素，排序完成。

   下面是堆排序数组的java实现代码：HeapSort进行构建大根堆并且实现堆中最大元素与最后一个元素的交换，BuildHeap实现构建大根堆

       public static void HeapSort(int[] array , int lengthIndex){
            // 将未排序数组构建大根堆
            BuildHeap(array,lengthIndex);
            // 交换堆中的根节点和最后一个节点
            int temp = array[lengthIndex];
            array[lengthIndex] = array[0];
            array[0] = temp;
            // 判断未排序元素是否大于一个
            if(lengthIndex > 0){
                 HeapSort(array, lengthIndex - 1);
            }   
        }
        
        // 构建大根堆
        public static void BuildHeap(int[] array,int lengthIndex){
            int temp = 0;
            // 循环堆中的所有父节点和它两个子节点进行比较，保证父节点是最大值
            for(int i = lengthIndex/2;i>=0;i--){
                if( (2*i+1) <= lengthIndex && array[i]<array[2*i+1] ){
                    temp = array[i];
                    array[i] = array[2*i+1];
                    array[2*i+1] = temp;
                }
                if((2*i+2) <= lengthIndex && array[i]<array[2*i+2] ){
                    temp = array[i];
                    array[i] = array[2*i+2];
                    array[2*i+2] = temp;
                }
            }
        }

   堆排序的空间复杂度为O(1),时间复杂度为O(nlogn)。