一、关于排序的一些基础介绍。
1.关于冒泡排序。
冒泡排序实际上只做教学使用,原理就是让数据的排序像泡泡一样逐渐变大,冒起来。
直接上简单代码:
public class bubbleSort {
public static void main(String[] args) {
int arrary[]={1,2,10,5,6,4,7,8};
int arrary2[]={9,2,3,5,1,6,4,7,8};
//初始排序自定义
for(int j=arrary.length;j>=0;j--){
for(int i=0;i<(arrary.length-1);i++){
//降序1`8
int a;
if(arrary[i]>arrary[i+1]){
a=arrary[i];
arrary[i]=arrary[i+1];
arrary[i+1]=a;
}
}
}
for(int i:arrary){
System.out.print(i+"+");
}
System.out.println("冒泡2");
myBubbleSort(arrary2);
for(int i=(arrary2.length-1);i>=0;i--){
System.out.print(arrary2[i]+"-");
}
}
public static void myBubbleSort(int[] a){
for(int j=0;j<a.length;j++){
for(int i=0;i<(a.length-1);i++){
//升序,小的冒起来
int b;
if(a[i]<a[i+1]){
b=a[i];
a[i]=a[i+1];
a[i+1]=b;
}
}
}
}
}
非常简单,只用两个循环,一个交换,就实现了基础冒泡排序。
2.快速排序
百度:它的基本思想是:通过一趟排序将要排序的数据分割成独立的两部分,其中一部分的所有数据都比另外一部分的所有数据都要小,然后再按此方法对这两部分数据分别进行快速排序,整个排序过程可以递归进行,以此达到整个数据变成有序序列。
上代码:
public class quickSort {
public static void main(String[] args) {
int arrary2[]={9,2,3,5,1,6,4,11,8};
quickSort(arrary2);
for(int i:arrary2){
System.out.print(i+" ");
}
}
/**
* 快速排序,使得整数数组 arr 有序
*/
public static void quickSort(int[] arr) {
if (arr == null || arr.length < 2) {
return;
}
quickSort(arr, 0, arr.length - 1);
}
/**
* 快速排序,使得整数数组 arr 的 [L, R] 部分有序
*/
public static void quickSort(int[] arr, int L, int R) {
if(L < R) {
// 把数组中随机的一个元素与最后一个元素交换,这样以最后一个元素作为基准值实际上就是以数组中随机的一个元素作为基准值
swap(arr, new Random().nextInt(R - L + 1) + L, R);
int[] p = partition(arr, L, R);
quickSort(arr, L, p[0] - 1);
quickSort(arr, p[1] + 1, R);
}
}
/**
* 分区的过程,整数数组 arr 的[L, R]部分上,使得:
* 大于 arr[R] 的元素位于[L, R]部分的右边,但这部分数据不一定有序
* 小于 arr[R] 的元素位于[L, R]部分的左边,但这部分数据不一定有序
* 等于 arr[R] 的元素位于[L, R]部分的中间
* 返回等于部分的第一个元素的下标和最后一个下标组成的整数数组
*/
public static int[] partition(int[] arr, int L, int R) {
int basic = arr[R];
int less = L - 1;
int more = R + 1;
while(L < more) {
if(arr[L] < basic) {
swap(arr, ++less, L++);
} else if (arr[L] > basic) {
swap(arr, --more, L);
} else {
L++;
}
}
return new int[] { less + 1, more - 1 };
}
/*
* 交换数组 arr 中下标为 i 和下标为 j 位置的元素
*/
public static void swap(int[] arr, int i, int j) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
}
这个需要自己去尝试理解了。
3.归并排序
直接上代码;
public static int[] sort(int[] a,int low,int high){
int mid = (low+high)/2; if(low<high){ sort(a,low,mid); sort(a,mid+1,high); //左右归并 merge(a,low,mid,high); } return a; } public static void merge(int[] a, int low, int mid, int high) { int[] temp = new int[high-low+1]; int i= low; int j = mid+1; int k=0; // 把较小的数先移到新数组中 while(i<=mid && j<=high){ if(a[i]<a[j]){ temp[k++] = a[i++]; }else{ temp[k++] = a[j++]; } } // 把左边剩余的数移入数组 while(i<=mid){ temp[k++] = a[i++]; } // 把右边边剩余的数移入数组 while(j<=high){ temp[k++] = a[j++]; } // 把新数组中的数覆盖nums数组 for(int x=0;x<temp.length;x++){ a[x+low] = temp[x]; } }(1)稳定性
归并排序是一种稳定的排序。
(2)存储结构要求
可用顺序存储结构。也易于在链表上实现。
(3)时间复杂度
对长度为n的文件,需进行趟二路归并,每趟归并的时间为O(n),故其时间复杂度无论是在最好情况下还是在最坏情况下均是O(nlgn)。
(4)空间复杂度
需要一个辅助向量来暂存两有序子文件归并的结果,故其辅助空间复杂度为O(n),显然它不是就地排序。
注意:
若用单链表做存储结构,很容易给出就地的归并排序
归并排序是一种稳定的排序。
(2)存储结构要求
可用顺序存储结构。也易于在链表上实现。
(3)时间复杂度
对长度为n的文件,需进行趟二路归并,每趟归并的时间为O(n),故其时间复杂度无论是在最好情况下还是在最坏情况下均是O(nlgn)。
(4)空间复杂度
需要一个辅助向量来暂存两有序子文件归并的结果,故其辅助空间复杂度为O(n),显然它不是就地排序。
注意:
若用单链表做存储结构,很容易给出就地的归并排序
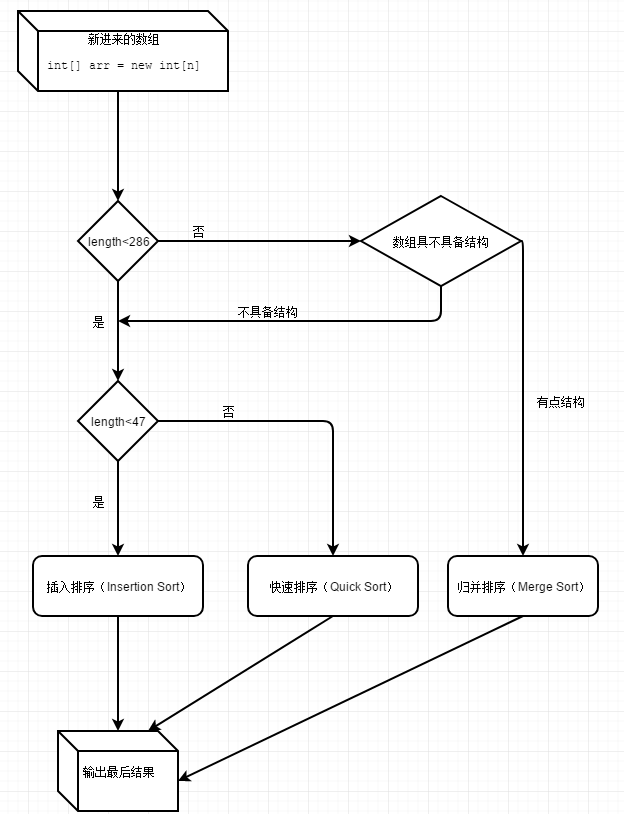
二、java中,arrary的sort算法是怎么样的。
如图:
源代码:
第一部分
@Override
@SuppressWarnings("unchecked")
public void sort(Comparator<? super E> c) {
final int expectedModCount = modCount;
Arrays.sort((E[]) elementData, 0, size, c);
if (modCount != expectedModCount) {
throw new ConcurrentModificationException();
}
modCount++;
}
第二部分
/**
* Sorts the specified range of the specified array of objects according
* to the order induced by the specified comparator. The range to be
* sorted extends from index {@code fromIndex}, inclusive, to index
* {@code toIndex}, exclusive. (If {@code fromIndex==toIndex}, the
* range to be sorted is empty.) All elements in the range must be
* <i>mutually comparable</i> by the specified comparator (that is,
* {@code c.compare(e1, e2)} must not throw a {@code ClassCastException}
* for any elements {@code e1} and {@code e2} in the range).
*
* <p>This sort is guaranteed to be <i>stable</i>: equal elements will
* not be reordered as a result of the sort.
*
* <p>Implementation note: This implementation is a stable, adaptive,
* iterative mergesort that requires far fewer than n lg(n) comparisons
* when the input array is partially sorted, while offering the
* performance of a traditional mergesort when the input array is
* randomly ordered. If the input array is nearly sorted, the
* implementation requires approximately n comparisons. Temporary
* storage requirements vary from a small constant for nearly sorted
* input arrays to n/2 object references for randomly ordered input
* arrays.
*
* <p>The implementation takes equal advantage of ascending and
* descending order in its input array, and can take advantage of
* ascending and descending order in different parts of the the same
* input array. It is well-suited to merging two or more sorted arrays:
* simply concatenate the arrays and sort the resulting array.
*
* <p>The implementation was adapted from Tim Peters's list sort for Python
* (<a href="http://svn.python.org/projects/python/trunk/Objects/listsort.txt">
* TimSort</a>). It uses techniques from Peter McIlroy's "Optimistic
* Sorting and Information Theoretic Complexity", in Proceedings of the
* Fourth Annual ACM-SIAM Symposium on Discrete Algorithms, pp 467-474,
* January 1993.
*
* @param <T> the class of the objects to be sorted
* @param a the array to be sorted
* @param fromIndex the index of the first element (inclusive) to be
* sorted
* @param toIndex the index of the last element (exclusive) to be sorted
* @param c the comparator to determine the order of the array. A
* {@code null} value indicates that the elements'
* {@linkplain Comparable natural ordering} should be used.
* @throws ClassCastException if the array contains elements that are not
* <i>mutually comparable</i> using the specified comparator.
* @throws IllegalArgumentException if {@code fromIndex > toIndex} or
* (optional) if the comparator is found to violate the
* {@link Comparator} contract
* @throws ArrayIndexOutOfBoundsException if {@code fromIndex < 0} or
* {@code toIndex > a.length}
*/
public static <T> void sort(T[] a, int fromIndex, int toIndex,
Comparator<? super T> c) {
if (c == null) {
sort(a, fromIndex, toIndex);
} else {
rangeCheck(a.length, fromIndex, toIndex);
if (LegacyMergeSort.userRequested)
legacyMergeSort(a, fromIndex, toIndex, c);
else
TimSort.sort(a, fromIndex, toIndex, c, null, 0, 0);
}
}
第三部分(算法1):
*/
public static void sort(Object[] a, int fromIndex, int toIndex) {
rangeCheck(a.length, fromIndex, toIndex);
if (LegacyMergeSort.userRequested)
legacyMergeSort(a, fromIndex, toIndex);
else
ComparableTimSort.sort(a, fromIndex, toIndex, null, 0, 0);
}
第三部分(算法2):
/**
* Checks that {@code fromIndex} and {@code toIndex} are in
* the range and throws an exception if they aren't.
*/
private static void rangeCheck(int arrayLength, int fromIndex, int toIndex) {
if (fromIndex > toIndex) {
throw new IllegalArgumentException(
"fromIndex(" + fromIndex + ") > toIndex(" + toIndex + ")");
}
if (fromIndex < 0) {
throw new ArrayIndexOutOfBoundsException(fromIndex);
}
if (toIndex > arrayLength) {
throw new ArrayIndexOutOfBoundsException(toIndex);
}
}
第三部分(算法3):
/** To be removed in a future release. */
private static <T> void legacyMergeSort(T[] a, int fromIndex, int toIndex,
Comparator<? super T> c) {
T[] aux = copyOfRange(a, fromIndex, toIndex);
if (c==null)
mergeSort(aux, a, fromIndex, toIndex, -fromIndex);
else
mergeSort(aux, a, fromIndex, toIndex, -fromIndex, c);
}
第三部分(算法)
/**
* Sorts the given range, using the given workspace array slice
* for temp storage when possible. This method is designed to be
* invoked from public methods (in class Arrays) after performing
* any necessary array bounds checks and expanding parameters into
* the required forms.
*
* @param a the array to be sorted
* @param lo the index of the first element, inclusive, to be sorted
* @param hi the index of the last element, exclusive, to be sorted
* @param c the comparator to use
* @param work a workspace array (slice)
* @param workBase origin of usable space in work array
* @param workLen usable size of work array
* @since 1.8
*/
static <T> void sort(T[] a, int lo, int hi, Comparator<? super T> c,
T[] work, int workBase, int workLen) {
assert c != null && a != null && lo >= 0 && lo <= hi && hi <= a.length;
int nRemaining = hi - lo;
if (nRemaining < 2)
return; // Arrays of size 0 and 1 are always sorted
// If array is small, do a "mini-TimSort" with no merges
if (nRemaining < MIN_MERGE) {
int initRunLen = countRunAndMakeAscending(a, lo, hi, c);
binarySort(a, lo, hi, lo + initRunLen, c);
return;
}
/**
* March over the array once, left to right, finding natural runs,
* extending short natural runs to minRun elements, and merging runs
* to maintain stack invariant.
*/
TimSort<T> ts = new TimSort<>(a, c, work, workBase, workLen);
int minRun = minRunLength(nRemaining);
do {
// Identify next run
int runLen = countRunAndMakeAscending(a, lo, hi, c);
// If run is short, extend to min(minRun, nRemaining)
if (runLen < minRun) {
int force = nRemaining <= minRun ? nRemaining : minRun;
binarySort(a, lo, lo + force, lo + runLen, c);
runLen = force;
}
// Push run onto pending-run stack, and maybe merge
ts.pushRun(lo, runLen);
ts.mergeCollapse();
// Advance to find next run
lo += runLen;
nRemaining -= runLen;
} while (nRemaining != 0);
// Merge all remaining runs to complete sort
assert lo == hi;
ts.mergeForceCollapse();
assert ts.stackSize == 1;
}
数量非常小的情况下(就像上面说到的,少于47的),插入排序等可能会比快速排序更快。 所以数组少于47的会进入插入排序。
快排数据越无序越快(加入随机化后基本不会退化),平均常数最小,不需要额外空间,不稳定排序。
归排速度稳定,常数比快排略大,需要额外空间,稳定排序。
所以大于或等于47或少于286会进入快排,而在大于或等于286后,会有个小动作:“// Check if the array is nearly sorted”。这里第一个作用是先梳理一下数据方便后续的归并排序,第二个作用就是即便大于286,但在降序组太多的时候(被判断为没有结构的数据,The array is not highly structured,use Quicksort instead of merge sort.),要转回快速排序。