P4525 【模板】自适应辛普森法1
题目描述
-
给定(a,b,c,d,L,R,)计算积分
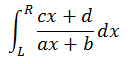
-
结果保留至小数点后6位。
-
数据保证计算过程中分母不为0且积分能够收敛。
输入格式
- 一行,包含(6)个实数(a,b,c,d,L,R)
输出格式
- 一行,积分值,保留至小数点后(6)位。
输入输出样例:
输入:
1 2 3 4 5 6
输出:
2.732937
题解
公式题,结论:
(intfrac{cx+d}{ax+b}dx=frac{(ad-bc)ln|ax+b|+acx}{a^2})
证明如下:((frac{(ad-bc)ln|ax+b|+acx}{a^2})')
(=frac{((ad-bc)ln|ax+b|)'+(acx)'}{a^2})
(=frac{(ad-bc)}{a^2}(ln|ax+b|)'+frac{c}{a})
设(f(x)=ln|x|,g(x)=ax+b,)
根据链式法则,((ln|ax+b|)'=(f(g(x)))'=g'(x) * f'(g(x))=a * frac{1}{ax+b})
∴原式 $ =frac{(ad-bc)}{a^2} * a * frac{1}{ax+b}+frac{c}{a}$
(=frac{(ad-bc)}{a} * frac{1}{ax+b}+frac{c}{a})
(=frac{ad-bc}{a(ax+b)}+frac{c}{a})
(=frac{ad-bc+c(ax+b)}{a(ax+b)})
(=frac{ad+acx}{a(ax+b)})
(=frac{d+cx}{ax+b})
证毕
坑
这题有坑我当然是理所当然的跳进去了
-
求((frac{1}{x})')时忘记套上绝对值,会 wa 两个点
-
(a=0)的时候需要特判,重新积分可得(intfrac{cx+d}{b}dx=int(frac{c}{b}x+frac{d}{b})dx=frac{c}{2b}x^2+frac{d}{b}x,)不这么做会 wa 四个点
代码
极其简单
#include<bits/stdc++.h>
using namespace std;
double a,b,c,d,l,r;
int main(){
cin>>a>>b>>c>>d>>l>>r;
if(a==0){
printf("%.6lf",(r*r-l*l)*c/b/2+d*(r-l)/b);
return 0;
}
printf("%.6lf",(a*c*(r-l)+(d*a-b*c)*(log(abs(a*r+b))-log(abs(a*l+b))))/a/a);
return 0;
}