题目描述
题目链接:https://www.luogu.org/problemnew/show/P1387
在一个n*m的只包含0和1的矩阵里找出一个不包含0的最大正方形,输出边长。
输入输出格式
输入格式:
输入文件第一行为两个整数n,m(1<=n,m<=100),接下来n行,每行m个数字,用空格隔开,0或1.
输出格式:
一个整数,最大正方形的边长
输入输出样例
输入样例#1:
4 4 0 1 1 1 1 1 1 0 0 1 1 0 1 1 0 1
输出样例#1:
2
算法解析:
来源:http://www.cnblogs.com/CXSheng/p/7801313.html
本题也可以参考洛谷题解
动态规划,求什么设什么。
设maxSize[i][j] = 以a[i][j]为右下角的最大正方形边长,
则maxSize[i][j] = k代表着a[i][j]左上方k*k区域内的数字都是1,
起初我想,如果a[i][j]是1,那么就可以把maxSize[i-1][j-1]代表的一大片矩形的边长扩大1.
即maxSize[i][j]=
① 0 ,a[i-1][j-1]==0 or 边界;
② maxSize[i-1][j-1]+1 , a[i-1][j-1]!=0;
但是!这是片面的,因为我忽略了a[i][j]正上方和正左方是否存在0的情况。
如图:

假设我们要求maxSize[i][j]对应着最右下角的红点,
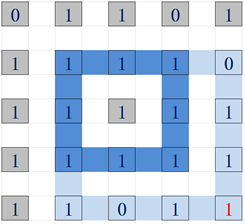
浅蓝色的圈是maxSize[i-1][j-1]对结果的影响;
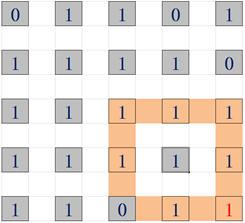
橙色的圈是a[i][j]正上方连续的1对结果的影响;
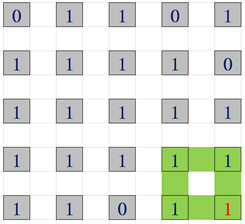
绿色的圈是a[i][j]正左方连续的1对结果的影响;
总图如下:
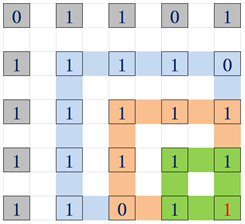
去三个值中最小的,记入maxSize[i][j]
综上可知,更新设定:
当a[i][j]为1时:
设maxSize[i][j] = 以a[i][j]为右下角的最大正方形边长,
LeftNum1[i][j] = a[i][j](不包括)正左边连续1的个数,
UpNum1[i][j] = a[i][j](不包括)正上方边连续1的个数,
于是maxSize[i][j] = min(maxSize[i-1][j-1]+1,leftNum1[i][j]+1,upNum1[i][j]+1)
注意边界情况即可。
1 #include<stdio.h> 2 #define MAXN 100 3 #define MAXM 100 4 int array[MAXN+1][MAXM+1]={0}; 5 int maxSize[MAXN+1][MAXM+1]={0}; 6 int leftNum1[MAXN+1][MAXM+1]={0}; 7 int upNum1[MAXN+1][MAXM+1]={0}; 8 int n,m; 9 int Figure(int tempN,int tempM) 10 { 11 if(tempN-1==0||tempM-1==0||array[tempN-1][tempM-1]==0) 12 return 1; 13 int min=maxSize[tempN-1][tempM-1]+1; 14 if(leftNum1[tempN][tempM]+1<min) 15 min=leftNum1[tempN][tempM]+1; 16 if(upNum1[tempN][tempM]+1<min) 17 min=upNum1[tempN][tempM]+1; 18 return min; 19 } 20 void tPrint() 21 { 22 /* int i,j; 23 printf(" "); 24 for(i=1;i<=n;i++) 25 { 26 for(j=1;j<=m;j++) 27 //printf("%d ",[i][j]); 28 printf("%d ",upNum1[i][j]);//============== 29 printf(" "); 30 } 31 printf(" ");*/ 32 } 33 int main() 34 { 35 int i,j; 36 scanf("%d%d",&n,&m); 37 int maxans=0; 38 for(i=1;i<=n;i++) 39 for(j=1;j<=m;j++) 40 scanf("%d",&array[i][j]); 41 for(i=1;i<=n;i++) 42 for(j=1;j<=m;j++) 43 { 44 if(j==1||array[i][j]==0) 45 leftNum1[i][j]=0; 46 else 47 { 48 if(array[i][j-1]==0) 49 leftNum1[i][j]=0; 50 else 51 leftNum1[i][j]=leftNum1[i][j-1]+1; 52 } 53 54 if(i==1||array[i][j]==0) 55 upNum1[i][j]=0; 56 else 57 { 58 if(array[i-1][j]==0) 59 upNum1[i][j]=0; 60 else 61 upNum1[i][j]=upNum1[i-1][j]+1; 62 } 63 } 64 for(i=1;i<=n;i++) 65 for(j=1;j<=m;j++) 66 { 67 maxSize[i][j]=Figure(i,j); 68 if(maxSize[i][j]>maxans) 69 maxans=maxSize[i][j]; 70 } 71 tPrint(); 72 printf("%d ",maxans); 73 return 0; 74 }
类似参考题目: