已知:
给一整数 n, 我们需要求前n个自然数形成的集合的所有可能子集中所有元素的和。
示例:
给出 n = 2, 返回 6 可能的子集为 {{1}, {2}, {1, 2}}. 子集的元素和为 1 + 2 + 1 + 2 = 6 给出 n = 3, 返回 24 可能的子集为 {{1}, {2}, {3}, {1, 2}, {1, 3}, {2, 3}, {1, 2, 3}} 子集的和为: 1 + 2 + 3 + (1 + 2) + (1 + 3) + (2 + 3) + (1 + 2 + 3) = 24
思路:
其实这更像是一个数学问题,而不是代码问题。以4为例子,取一个数,则取1的可能性为1种,取两个数字,则取1的可能性为3种,取三个数字,则取1的可能性为3种,
取四个数字,可能性为1种,则1总共计算了 1+3+3+1 共8次, 其他三个数字也是8次。 所以,结合上面两个示例,很容易可以推的: 当已知n的值时,我们会取里面的每个数字2^(n-1)次
上述分析来源:http://blog.csdn.net/mio_bass/article/details/78797298
根据上述分析,求解的公式就是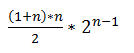
公式解析:因为最后把所有子集的所有项累加的表达式里面,1~n的每一个数都有机会出现2^(n-1)次,所以求和表达式就变为:
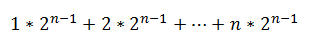
最终变为上面第一个公式。
利用第一个公式求解就非常方便了。
补充:
对于“会取里面的每个数字2^(n-1)次”的另一种解析可以如下进行:
集合里面有1~n共n个元素。构造子集的时候,对每个元素而言都有取或不取两种选择,所以子集数目共有2^(n-1)个。
讨论这些子集:原集合的元素ai只有选和不选两种情况,故所有子集分两类:包含ai的子集和不包含ai的子集。每一类的子集个数都是2^(n-1)个。
所以最后面计算累加和的时候需要累加ai的次数是2^(n-1)次,也就是元素ai对累加和的贡献是ai*2^(n-1)。
每一个元素出现的次数都是2^(n-1)次,所以上述第二个公式即可推出来。
代码比较简单就不写了。
其他参考:
http://blog.csdn.net/zhaohengchuan/article/details/78716365
http://blog.csdn.net/u010005161/article/details/52175525