算法@贪心算法

Dijkstra 求单源最短路径问题

假如你现在在华山景区任意一个景点处，如何找到通往所有景点的最短路径呢？
荷兰的 艾兹格 W 迪科斯彻 解决了这个问题...

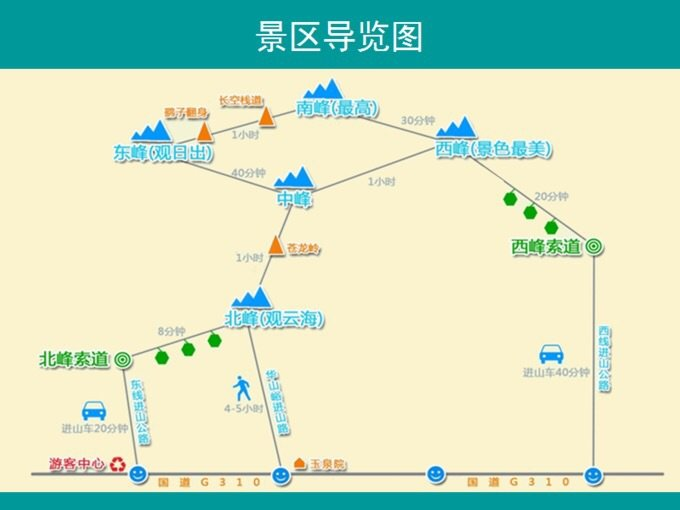
把景点和距离抽象为，类似下面的有向图/无向图，用邻接矩阵存储数据。

从当前所在位置源点u开始
（1）初始化----每个点到u的最短距离dist[i] = map[u][i] 集合S={源点u} 集合V_S={除源点u外的所有顶点}
（2）找最小----在集合V_S找到和源点相连的最近的顶点a
（3）加入S战队----把a从V_S中取出放到S中
（4）判断结束----如果V_S为空则算法结束
（5）借东风----借助a走捷径，如果其他顶点x经过a后的距离dist[a]+map[a][x]小于其他路线的距离dist[x]，则更新dist[x]为此时的短距离，并把x的前驱节点p[x]=a
（6）跳转到（2）

如上图从1开始走
--------------V_S={2，3, 4， 5}中2距离1最近则
1-2
和2直接相连的3、4暂时均可走捷径则更新dist[3],dist[4]
1-2-3
1-2-4
--------------V_S={3,4,5}中3距离1最近则
1-2-3
和3相连的4、5中5暂时可以走捷径则更新dist[5]
--------------V_S={4,5}中5距离1最近则
1-2-3-5
--------------V_S={4}中4距离1最近(只剩4了)
--------------V_S={}为空，算法结束

最终结果
1-2
1-2-3
1-2-4
1-2-3-5

# -*- coding: utf-8 -*-
# @Time : 2021/8/23 14:37
# @Author : HUGBOY
# @File : Dijkstra.py
# @Software: PyCharm

INF = float("inf")  # 正无穷大
S = set()  # 集合
V_S = set()  # 集合

Encode = {  # 景点代号
    1: '玉泉院', 2: '北峰', 3: '苍龙岭', 4: '金锁关',
    5: '东峰', 6: '长空栈道鹞子翻身', 7: '南峰', 8: '中锋',
    9: '西峰', 10: '西索道', 11: '游客中心', 12: '北索道'
}


def Dijkstra(u):
    # 初始化
    for i in range(1, N + 1):
        V_S.add(i)
        Dist[i] = Map[u][i]
        if Dist[i] == INF:  # 与源点u不相邻
            P[i] = -1
        else:  # 与源点u相邻
            P[i] = u

    Dist[u] = 0  # u到源点距离为0
    S.add(u)  # 初始时集合S中只有一个元素: 源点u
    V_S.remove(u)  # 集合V_S有除源点u之外的所有元素

    for i in range(1, N + 1):
        temp = INF
        t = u

        #  从V_S中寻找距离源点最近的景点t "找最小"
        for j in V_S:
            if Dist[j] < temp:
                t = j
                temp = Dist[j]
        if t == u:
            return
        else:
            S.add(t)
            V_S.remove(t)

        #  更新邻接景点t的景点的数据 "借东风"
        for j in V_S:
            if Map[t][j] < INF:
                if Map[t][j] + Dist[t] < Dist[j]:
                    Dist[j] = Map[t][j] + Dist[t]
                    P[j] = t

def Display(u):

    print("从 %s 出发到达各个景点的 最短时间 及 路线" % Encode[u])
    for i in range(1, N+1):
        if Dist[i] == INF:
            print("sorry, 目的地 %d %s 不可达 !" % (i, Encode[i]))
        else:
            print("[%d]%s 最短时间: %d min " % (i, Encode[i], Dist[i]))
            FindPath(i)

def FindPath(i):
    x = P[i]
    stack = []
    print("路线:")
    while x != -1:
        stack.append(x)
        x = P[x]
    while len(stack):
        print('%s-- ' % (Encode[stack[-1]]), end='')
        stack.pop()
    print(Encode[i])

if __name__ == '__main__':

    N = 12
    M = 16

    # N = int(input("请输入景点个数: 	"))
    # M = int(input("请输入景点之间的路线个数: 	"))

    # 初始化 N*N邻接矩阵 初始值为正无穷，景区编号从1开始 0行、0列的值无意义
    # Map = [[INF] * (N + 1) for i in range(N + 1)]

    # while M:
    #     u, v, w = input("请输入景点之间的路线及距离: 	").split()
    #     u, v, w = int(u), int(v), int(w)
    #     Map[u][v] = min(Map[u][v], w)  # 取最小值
    #     Map[v][u] = min(Map[v][u], w)
    #     M -= 1

    inf = INF
    Map = [[inf, inf, inf, inf, inf, inf, inf, inf, inf, inf, inf, inf, inf], [inf, inf, 360, inf, inf, inf, inf, inf, inf, inf, inf, inf, inf], [inf, 360, inf, 75, inf, inf, inf, inf, inf, inf, inf, inf, 5], [inf, inf, 75, inf, 75, inf, inf, inf, inf, inf, inf, inf, inf], [inf, inf, inf, 75, inf, 40, inf, inf, 20, 40, inf, inf, inf], [inf, inf, inf, inf, 40, inf, 20, inf, 30, inf, inf, inf, inf], [inf, inf, inf, inf, inf, 20, inf, 20, inf, inf, inf, inf, inf], [inf, inf, inf, inf, inf, inf, 20, inf, 30, 40, inf, inf, inf], [inf, inf, inf, inf, 20, 30, inf, 30, inf, 30, inf, inf, inf], [inf, inf, inf, inf, 40, inf, inf, 40, 30, inf, 5, inf, inf], [inf, inf, inf, inf, inf, inf, inf, inf, inf, 5, inf, 40, inf], [inf, inf, inf, inf, inf, inf, inf, inf, inf, inf, 40, inf, 20], [inf, inf, 5, inf, inf, inf, inf, inf, inf, inf, inf, 20, inf]]

    Dist = [INF] * (N + 1)  # 到源点最短距离
    P = [0] * (N + 1)  # 最短距离路线终点景点的 前驱景点

    st = int(input("请输入您当前所在位置代号: 	"))
    Dijkstra(st)
    Display(st)

D:pythonpython.exe E:/PYTHON/Class/ALG/趣学算法/Dijkstra.py
请输入您当前所在位置代号: 	7
从 南峰 出发到达各个景点的 最短时间 及 路线
[1]玉泉院 最短时间: 470 min 
路线:
南峰-- 西峰-- 西索道-- 游客中心-- 北索道-- 北峰-- 玉泉院
[2]北峰 最短时间: 110 min 
路线:
南峰-- 西峰-- 西索道-- 游客中心-- 北索道-- 北峰
[3]苍龙岭 最短时间: 125 min 
路线:
南峰-- 中锋-- 金锁关-- 苍龙岭
[4]金锁关 最短时间: 50 min 
路线:
南峰-- 中锋-- 金锁关
[5]东峰 最短时间: 40 min 
路线:
南峰-- 长空栈道鹞子翻身-- 东峰
[6]长空栈道鹞子翻身 最短时间: 20 min 
路线:
南峰-- 长空栈道鹞子翻身
[7]南峰 最短时间: 0 min 
路线:
南峰
[8]中锋 最短时间: 30 min 
路线:
南峰-- 中锋
[9]西峰 最短时间: 40 min 
路线:
南峰-- 西峰
[10]西索道 最短时间: 45 min 
路线:
南峰-- 西峰-- 西索道
[11]游客中心 最短时间: 85 min 
路线:
南峰-- 西峰-- 西索道-- 游客中心
[12]北索道 最短时间: 105 min 
路线:
南峰-- 西峰-- 西索道-- 游客中心-- 北索道

Process finished with exit code 0

HuffmanCode 哈夫曼编码问题（不等长编码）

# -*- coding: utf-8 -*-
# @Time : 2021/8/24 20:19
# @Author : HUGBOY
# @File : HuffCode.py
# @Software: PyCharm

#  节点 数据结构
class HNodeType(object):
    def __init__(self, weight, parent, lchild, rchild):
        self.weight = weight
        self.parent = parent
        self.lchild = lchild
        self.rchild = rchild
        self.value = ''

#  编码 数据结构
class HCodeType(object):
    def __init__(self):
        self.bit = []
        #self.start = start

#  构造哈夫曼树
def HuffmanTree(HuffNode, N):
    #  初始化哈夫曼树列表中的节点
    for i in range(2 * N - 1):  # N个叶子 => 2*N - 1 个节点
        node = HNodeType(0, -1, -1, -1)  # 参数: 权值 双亲 左孩子 右孩子
        HuffNode.append(node)

    #  输入叶子节点权值
    for i in range(N):
        value, weight = input("请输入第%d个叶子的 字符 权值>>" % (i + 1)).split()
        HuffNode[i].value, HuffNode[i].weight = str(value), float(weight)

    #  构造 Huffman 树

    for i in range(N - 1):  # 2*N - 1 - N 即 N - 1 个双亲节点，需要执行N - 1次树的合并
        w1 = w2 = MAXWEIGHT  # 两个最小树的权值
        ind1 = ind2 = -1  # 两个最小树的双亲

        #  找两个最小且无双亲的节点合并
        for j in range(N + i):
            if HuffNode[j].parent == -1:
                if HuffNode[j].weight < w1:
                    # 把旧最小信息w2 ind2
                    w2 = w1
                    ind2 = ind1
                    # 把新最小信息w1 ind1
                    w1 = HuffNode[j].weight
                    ind1 = j

                elif HuffNode[j].weight < w2:
                    w2 = HuffNode[j].weight
                    ind2 = j

        HuffNode[ind1].parent = N + i
        HuffNode[ind2].parent = N + i
        #  设置合并后生成的节点
        HuffNode[N + i].parent = -1
        HuffNode[N + i].weight = w1 + w2
        HuffNode[N + i].lchild = ind1
        HuffNode[N + i].rchild = ind2

        print("第%d轮 %.2f 与 %.2f 合并啦 !" % (i+1, HuffNode[ind1].weight, HuffNode[ind2].weight))

#  哈夫曼树编码
def HuffmanCode(HuffCode, N):

    #  初始化哈夫曼编码节点
    for i in range(N):
        node = HCodeType()
        HuffCode.append(node)



    for i in range(N):
        temp = HCodeType()  # 临时存放某字符编码
        c = i
        p = HuffNode[c].parent
        while p != -1:
            if HuffNode[p].lchild == c:
                temp.bit.append(0)
            else:
                temp.bit.append(1)
            #temp.start -= 1
            c = p
            p = HuffNode[c].parent
        #  保存叶子节点的编码到HuffCode中

        HuffCode[i].bit = temp.bit

        #HuffCode[i].start = temp.start


if __name__ == '__main__':

    MAXLEAF = 30  # 叶子数 (待编码字符个数)
    HuffNode = []  # 哈夫曼树节点
    HuffCode = []  # 哈夫曼编码节点
    #MAXBIT = 100
    MAXWEIGHT = 10000
    MAXNODE = 2 * MAXLEAF - 1

    N = int(input("请输入叶子数 N>>"))
    HuffmanTree(HuffNode, N)
    HuffmanCode(HuffCode, N)

    for i in range(N):
        print(HuffNode[i].value, HuffCode[i].bit)

D:pythonpython.exe E:/PYTHON/Class/ALG/趣学算法/HuffCode.py
请输入叶子数 N>>6
请输入第1个叶子的 字符 权值>>a 0.05
请输入第2个叶子的 字符 权值>>b 0.32
请输入第3个叶子的 字符 权值>>c 0.18
请输入第4个叶子的 字符 权值>>d 0.07
请输入第5个叶子的 字符 权值>>e 0.25
请输入第6个叶子的 字符 权值>>f 0.13
第1轮 0.05 与 0.07 合并啦 !
第2轮 0.12 与 0.13 合并啦 !
第3轮 0.18 与 0.25 合并啦 !
第4轮 0.25 与 0.32 合并啦 !
第5轮 0.43 与 0.57 合并啦 !
a [0, 0, 0, 1]
b [1, 1]
c [0, 0]
d [1, 0, 0, 1]
e [1, 0]
f [1, 0, 1]

Process finished with exit code 0

Prim 最小生成树问题

#-*- coding: utf-8 -*-
#@Time : 2021/8/25 19:11
#@Author : HUGBOY
#@File : Prim.py
#@Software: PyCharm



def Prim(N, u0, C):

    # 初始化closeV closeLen
    for i in range(N):
        closeV[i] = u0
        closeLen[i] = C[u0][i]
        if i == u0:
            closeLen[i] = 0
    #  从指定位置u0开始寻找
    U.add(u0)
    V_U = V - U
    for _ in range(N):  # 循环N次 U最多添加N个顶点元素

        temp = INF
        t = u0
        # 在V_U中找距离集合U最近(边长最小)的顶点t 放到U
        for i in V_U:
            if closeLen[i] < temp:
                t = i           #  记录该顶点 更新temp
                temp = closeLen[i]

        if t == u0:  # 未找到
            break

        U.add(t)
        print(t)
        V_U.remove(t)

        # 更新closeV minLen 的值
        for j in V_U:
            if C[t][j] < closeLen[j]:
                closeLen[j] = C[t][j]
                closeV[j] = t

if __name__ == '__main__':

    INF = float("inf")  # 无穷大
    U = set()  # 集合

    N, M = input("请输入 顶点数 边数>>>").split()
    N, M = int(N), int(M)

    C = [[INF] * N for i in range(N)]  # N*N 邻接矩阵C[n][n]

    for i in range(M):
        u, v, w = input("请输入第%d条边 顶点 顶点 权值>>>" % (i+1)).split()  # 顶点从1开始数
        C[int(u)-1][int(v)-1] = int(w)
        C[int(v)-1][int(u)-1] = int(w)

    # inf = INF
    # C = [[inf, 23, inf, inf, inf, 28, 36], [inf, inf, 20, inf, inf, inf, 1], [inf, inf, inf, 15, inf, inf, 4], [inf, inf, inf, inf, 3, inf, 9], [inf, inf, inf, inf, inf, 17, 16], [inf, inf, inf, inf, inf, inf, 25], [inf, inf, inf, inf, inf, inf, inf]]

    u0 = int(input("请输入 任意顶点u0>>>")) - 1


    closeV = [u0] * N  # 临近点(和自己相连边长最小的点)
    closeLen = [INF] * N  # 临近距离
    V = {i for i in range(N)}  # 顶点全集

    print(V, U)
    Prim(N, u0, C)
    print("closeLen[]	", closeLen)

D:pythonpython.exe E:/PYTHON/Class/ALG/Prim.py
请输入 顶点数 边数>>>7 12
请输入第1条边 顶点 顶点 权值>>>1 2 23
请输入第2条边 顶点 顶点 权值>>>1 6 28
请输入第3条边 顶点 顶点 权值>>>1 7 36
请输入第4条边 顶点 顶点 权值>>>2 3 20
请输入第5条边 顶点 顶点 权值>>>2 7 1
请输入第6条边 顶点 顶点 权值>>>3 4 15
请输入第7条边 顶点 顶点 权值>>>3 7 4
请输入第8条边 顶点 顶点 权值>>>4 5 3
请输入第9条边 顶点 顶点 权值>>>4 7 9
请输入第10条边 顶点 顶点 权值>>>5 6 17
请输入第11条边 顶点 顶点 权值>>>5 7 16
请输入第12条边 顶点 顶点 权值>>>6 7 25
请输入 任意顶点u0>>>1
{0, 1, 2, 3, 4, 5, 6} set()
1
6
2
3
4
5
closeLen[]	 [0, 23, 4, 9, 3, 17, 1]

Process finished with exit code 0