机器学习 之XGBoost算法

目录

• 1、基本知识点简介
• 2、XGBoost提升树算法
  • 2.1 XGBoost原理
  • 2.2 XGBoost中损失函数的泰勒展开
  • 2.3 XGBoost中正则化项的选定
  • 2.4 最终的目标损失函数及其最优解的表达形式

1、基本知识点简介

• 在集成学习的Boosting提升算法中，有两大家族：第一是AdaBoost提升学习方法，另一种是GBDT梯度提升树。

• 传统的AdaBoost算法：利用前一轮迭代弱学习器的误差来更新训练集的权重，一轮轮迭代下去。

• 梯度提升树GBDT：也是通过迭代的算法，使用前向分布算法，但是其弱分类器限定了只能使用CART回归树模型。

• GBDT算法原理：指通过在残差减小的梯度方向建立boosting tree（提升树），即gradient boosting tree（梯度提升树）。每次建立新模型都是为了使之前模型的残差往梯度方向下降。

• XGBoost原理：XGBoost属于集成学习Boosting，是在GBDT的基础上对Boosting算法进行的改进，并加入了模型复杂度的正则项。GBDT是用模型在数据上的负梯度作为残差的近似值，从而拟合残差。XGBoost也是拟合数据残差，并用泰勒展开式（二阶泰勒展开式）对模型损失残差的近似，同时在损失函数上添加了正则化项。

2、XGBoost提升树算法

• 由于在第 n 棵树训练时，需要用到第n-1棵树的（近似）残差，存在依赖关系，因此GBDT难以实现分布式（也可以实现，但是比较麻烦）。
• XGBoost整个过程包括：原始公式表达+泰勒展开式+正则化项的选定+最终目标函数的确定

2.1 XGBoost原理

• XGBoost原理：XGBoost属于集成学习Boosting，是在GBDT的基础上对Boosting算法进行的改进，并加入了模型复杂度的正则项。GBDT是用模型在数据上的负梯度作为残差的近似值，从而拟合残差。XGBoost也是拟合数据残差，但其采用泰勒展开式对模型损失残差的近似，同时在损失函数上添加了正则化项。

[Obj^{t} = sum_{i=1}^{n} L(y_{i}, hat{y}_{i}^{(t-1)} + f_{t}(x_{i})) + Omega (f_{t}) + constant ]

其中(sum_{i=1}^{n} L(y_{i}, hat{y}_{i}^{(t-1)}))为损失函数，(t-1)指第(t-1)棵树；(Omega (f_{t}))为正则项，包括L1、L2；(constant)为常数项。??

2.2 XGBoost中损失函数的泰勒展开

• 泰勒展开式定义：(f(x+Delta x) simeq f(x) + f^{'}(x) Delta x + frac{1}{2} f^{''}(x) Delta x^{2})

此处(f(x, x+Delta x))-----(L(y_{i}, hat{y}_{i}^{(t-1)} + f_{t}(x_{i})))，即将(f_{t}(x_{i}))视为(Delta x)，将$hat{y}_{i}^{(t-1)} (视为)x(，将)L(函数视为)f$函数。

因此定义一阶导数(g_{i} = partial_{hat{y}^{(t-1)}} l(y_{i}, hat{y}^{(t-1)}))，二阶导数(h_{i} = partial_{hat{y}^{(t-1)}}^{2} l(y_{i}, hat{y}^{(t-1)}))，则有：

[Obj^{t} = sum_{i=1}^{n} [l(y_{i}, hat{y})_{i}^{(t-1)} +g_{i} f_{t}(x_{i}) + frac{1}{2} h_{i} f_{t}^{2}(x_{i})] + Omega (f_{t}) + constant ]

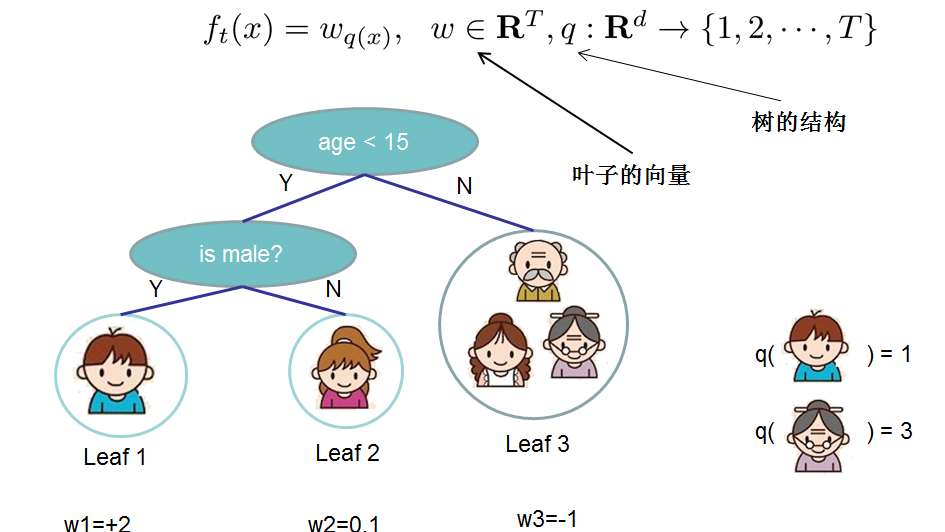
• 对于 f 的定义，我们把树拆分成结构部分(q)和叶子权重部分(omega)。结构函数q把输入映射到叶子的索引号上面去，而(omega)给定了每个索引号对应的叶子分数是多少？

[f_{t}(x) = omega_{q}(x), omega in R^{T}, q:R^{d} o {1,2,...,T} ]

2.3 XGBoost中正则化项的选定

• 正则化项的选定：定义CART决策树中里面的叶子结点个数为T，每个叶子结点上面输出分数的L2模平方。有：

[Omega (f_{t}) = gamma T + frac{1}{2}lambda sumlimits_{j=1}^{T} omega_{j}^{2} ]

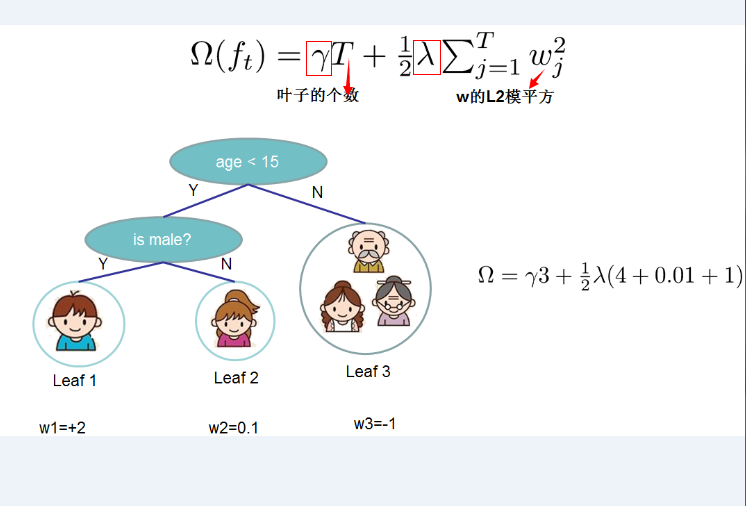
其中(gamma)和(lambda)是控制比重参数。定义每个叶子上面样本集合为(I_{j} = {i | q(x_{i}) = j})，即能个到达这个叶子结点上的所有特征结点，对应权重为(omega_{j})，则目标函数（损失函数）变为：

[Obj^{(t)} simeq sumlimits_{i=1}^{n} [g_{i} f_{t}^(x_{i} + frac{1}{2} h_{i} f_{t}^{2} (x_{i}))] + Omega(f_{t}) \ = sumlimits_{i=1}^{n} [g_{i} omega_{q}(x_{i}) + frac{1}{2} h_{i} omega_{q}^{2}(x_{i})] + gamma T + frac{1}{2} lambda sumlimits_{j=1}^{T} omega_{j}^{2} \ = sumlimits_{j=1}^{T} [(sum_{i in I_{j}} g_{i}) omega_{j} + frac{1}{2} (sum_{i in I_{j}} h_{i} + lambda) omega_{j}^{2}] + lambda T ]

其中 n 表示第 n 棵树，T表示树中叶子结点个数。

• 这一目标包含了T个相互独立的单变量二次函数，我们定义：

[G_{j} = sum_{i in I_{j}} g_{i}, i=1,2,...,n; j=1,2,..,T ]

[H_{j} = sum_{i in I_{j}} h_{i}, i=1,2,...,n; j=1,2,..,T ]

这里(G_{j})为该叶子结点上面样本集合中数据点在误差函数上的一阶导数和二阶导数。

2.4 最终的目标损失函数及其最优解的表达形式

• 最终公式可以化简为：

[Obj^{(t)} = sumlimits_{j=1}^{T} [(sum_{i in I_{j}} g_{i}) omega_{j} + frac{1}{2} (sum_{i in I_{j}} h_{i} + lambda) omega_{j}^{2}] + lambda T \ = sumlimits_{j=1}^{T} [G_{j} omega_{j} + frac{1}{2} (H_{j} + lambda) omega_{j}^{2} + lambda T] ]

• 通过令(Obj^{t})对(omega_{j})求导等于0，可以得到

[omega_{j}^{*} = - frac{G_{j}}{H_{j} + lambda} ]

• 然后把(omega_{j})最优解代入得到：

[Obj = - frac{1}{2} sumlimits_{j=1}^{T} frac{G_{j}^{2}}{H_{j} + lambda} + gamma T ]

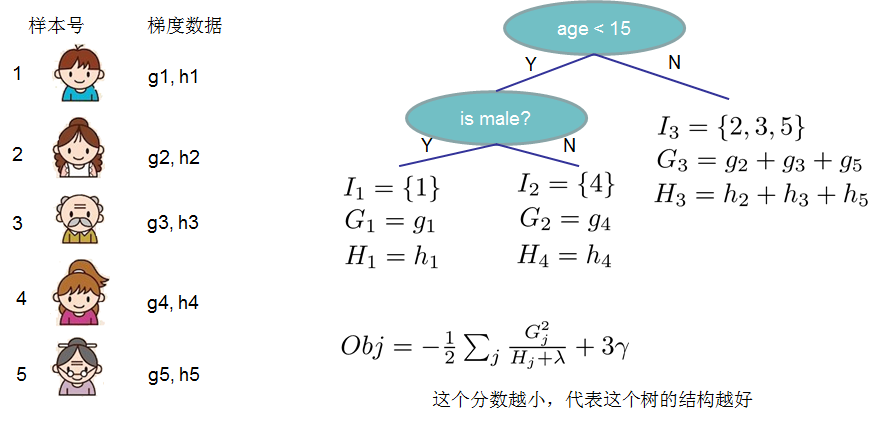
• 结构分数：Obj代表了当我们制定一个树的结构时，目标最多能减少多少，即取最优解，被成为结构分数。
  

• 贪心法：指每一次尝试去对已有的叶子加入一个分割。得到的增益为：

[Gain = frac{1}{2} [frac{G_{L}^{2}}{H_{L} + lambda} + frac{G_{R}^{2}}{H_{R} + lambda} - frac{(G_{L}+G_{R})^{2}}{H_{L} + H_{R} + lambda}] - lambda ]

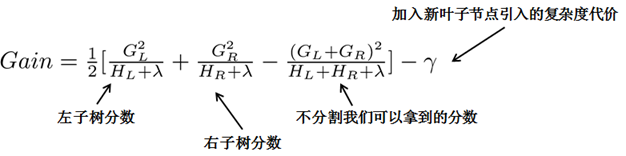
对于每次扩展，我们都需要枚举所有可能的分割方案，例如，通过枚举所有x<a这样的条件，对于某个特定的分割a，我们要计算a左边和右边的导数和。

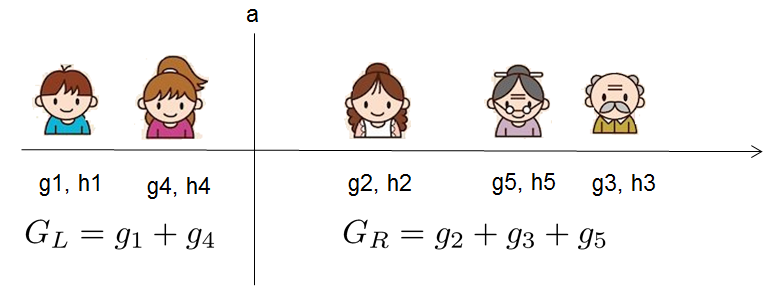
我们只要做一遍从左到右的扫描就可以枚举出所有分割的梯度和GL和GR，然后用上面的公式计算每个分割方案的分数增益就可以了。

• 重点：通过引入新叶子的惩罚项(lambda)，可以优化这个目标函数，对应于决策树的剪枝。当引入的分割带来的增益小于一个阈值的时候，我们就可以剪掉这个分割。（正式推导目标时，计算分数和剪枝这样的策略都能以公式呈现，而不是启发式。）

参考：
1、XGBoost：https://www.cnblogs.com/zhouxiaohui888/p/6008368.html